题目内容
12．
在5×5的正方形网格中，每个小正方形的边长为1，用四边形覆盖如图所示，被覆盖的网格线中，竖直部分的线段的长度之和记作m，水平部分的线段的长度之和记作n，则m-n=（ ）| A． | 0 | B． | 0.5 | C． | -0.5 | D． | 0.75 |
分析 根据平行线等分线段定理，梯形中位线定理、三角形中位线定理，分别求出m、n即可解决问题，
解答 解：如图
在△ACD中，易知DF=3，PM=$\frac{1}{2}$DF=$\frac{3}{2}$，
又PM=$\frac{1}{2}$（EG+QT），
∴EG+QT=3，
∴EG+PM+QT+FD=$\frac{15}{2}$，
易知MN=$\frac{1}{3}$AC，GH=$\frac{2}{3}$AC，
∴AC+GH+MN=10，
用此方法可得m=$\frac{25}{2}$，n=$\frac{25}{2}$，
∴m-n=0，
故选A．
点评 本题考查平行线等分线段定理、三角形中位线定理、梯形中位线定理等知识，解题的关键是学会灵活运用所学知识解决问题，属于中考创新题目．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
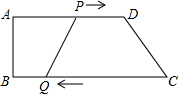如图1，四边形ABCD中，AD∥BC，∠B=90°，AD=18，BC=21．点P从A出发沿AD以每秒1个单位的速度向点D匀速移动，点Q从点C沿CB以每秒2个单位的速度向点B匀速移动．点P、Q同时出发，其中一个点到终点时两点停止运动，设移动的时间为t秒．求：
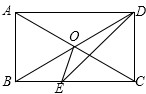如图，矩形ABCD中，AC、BD交于点O，∠AOB=60°，DE平分∠ADC交BC于点E，连接OE，则∠COE=75°．
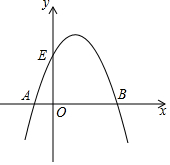已知抛物线经过点A（-1，0），B（3，0），C（1，4），与y轴交于点E．
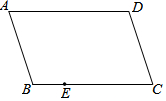如图，四边形ABCD是平行四边形，E是BC边上一点，只用一把无刻度的直尺在AD边上作点F，使得DF=BE．
如图，四边形ABCD是正方形，CF∥BD，DF∥BE，若BE=BD，则∠CDF=105°．
2．汽车公司有甲、乙两种货车可供租用，现有一批货物要运往某地，货主准备租用该公司货车，已知以往甲、乙两种货车运货情况如表：
（1）甲、乙两种货车每辆可装多少吨货物？
（2）若货主需要租用该公司的甲种货车8辆，乙种货车6辆，刚好运完这批货物，如按每吨付运费50元，则货主应付运费总额为多少元？
（3）若货主共有20吨货，计划租用该公司的货车正好（每辆车都满载）把这批货运完，该汽车公司共有哪几种运货方案？
| 第一次 | 第二次 | |
| 甲种货车（辆） | 2 | 5 |
| 乙种货车（辆） | 3 | 6 |
| 累计运货（吨） | 13 | 28 |
（2）若货主需要租用该公司的甲种货车8辆，乙种货车6辆，刚好运完这批货物，如按每吨付运费50元，则货主应付运费总额为多少元？
（3）若货主共有20吨货，计划租用该公司的货车正好（每辆车都满载）把这批货运完，该汽车公司共有哪几种运货方案？