题目内容
17.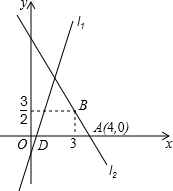 如图,直线l1的解析表达式为y=3x-3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
如图,直线l1的解析表达式为y=3x-3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.(1)求点D的坐标;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标;
(4)在坐标平面内是否存在这样的点H,使以A,D,C,H为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点H的个数.
分析 (1)令y=0,求出x的值即可得出D点坐标;
(2)先利用待定系数法求出直线l2的解析式,故可得出C点坐标,根据三角形的面积公式即可得出结论;
(3)根据△ADP与△ADC的高相等即可得出结论;
(4)分AD是平行四边形的边与对角线两种情况进行讨论.
解答 解:(1)∵令y=0,则x=1,
∴D(1,0);
(2)设直线l2的解析式为y=kx+b(k≠0),
∵A(4,0),B(3,$\frac{3}{2}$),
∴$\left\{\begin{array}{l}0=4k+b\\ \frac{3}{2}=3k+b\end{array}\right.$,解得$\left\{\begin{array}{l}k=-\frac{3}{2}\\ b=6\end{array}\right.$,
∴直线l2的解析式为y=-$\frac{3}{2}$x+6,
∴$\left\{\begin{array}{l}y=3x-3\\ y=-\frac{3}{2}x+6\end{array}\right.$,解得$\left\{\begin{array}{l}x=2\\ y=3\end{array}\right.$,
∴C(2,3).
∵AD=4-1=3,
∴S△ADC=$\frac{1}{2}$×3×3=$\frac{9}{2}$;
(3)∵△ADP与△ADC的底相同,
∴其高相等,
∴当y=-3即-$\frac{3}{2}$x+6=-3时,x=6,
∴P(6,-3);
(4)存在.
设H(a,b),
当AD为平行四边形的边时,
∵AD∥CH,AD=CH=3,A(4,0),D(1,0),C(2,3),
∴H1(5,3),H2(-1,3);
当AD为平行四边形的对角线时,
$\frac{1+4}{2}$=$\frac{2+a}{2}$,$\frac{3+b}{2}$=0,解得a=3,b=-3,
∴H3(3,-3).
∴满足条件的点H的个数是3个.
点评 本题考查的是一次函数综合题,涉及到一次函数图象上点的坐标特点、平行四边形的判定与性质等知识,在解答(3)时要注意进行分类讨论.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案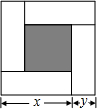 如图,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个相同长方形的两边长(x>y),给出以下关系式:①x+y=m;②x-y=n;③xy=$\frac{{m}^{2}-{n}^{2}}{4}$. 其中正确的关系式的个数有( )
如图,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个相同长方形的两边长(x>y),给出以下关系式:①x+y=m;②x-y=n;③xy=$\frac{{m}^{2}-{n}^{2}}{4}$. 其中正确的关系式的个数有( )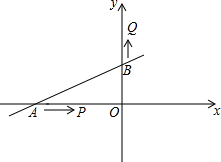 直线y=$\frac{1}{2}$x+2交x轴于A,交y轴于B,P点从A点出发沿射线AO运动,同时Q从B点出发沿射线OB方向运动,速度均为1个单位/秒
直线y=$\frac{1}{2}$x+2交x轴于A,交y轴于B,P点从A点出发沿射线AO运动,同时Q从B点出发沿射线OB方向运动,速度均为1个单位/秒 如图,∠A=29°,∠C′=62°,△ABC与△A′B′C′关于直线l对称,则∠B=89°.
如图,∠A=29°,∠C′=62°,△ABC与△A′B′C′关于直线l对称,则∠B=89°.
 利用平移求图中图形的周长.
利用平移求图中图形的周长.