题目内容
6．若函数y=-x2-2ax（0≤x≤1）的最大值为a2，求实数a的取值范围．分析 根据函数的解析式求得顶点坐标，从而求得对称轴和函数的最大值，然后根据已知条件即可求得．
解答 解：∵函数y=-x2-2ax=-（x+a）2+a2，
∴函数的对称轴x=-a，最大值为为a2，
∵0≤x≤1时的最大值为a2，
∴0＜-a＜1，
故实数a的取值范围是-1＜a＜0．
点评 本题考查了二次函数的性质以及二次函数的最值，根据题意得出0＜-a＜1是解题的关键．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
如图，正方形ABCD的边长是5cm，以直线AB为轴，将正方形旋转一周，所得几何体的左视图的面积是50cm2 （结果保留π）．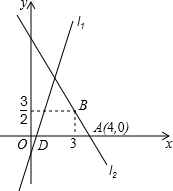
如图，直线l1的解析表达式为y=3x-3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．
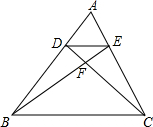如图，在△ABC中，DE∥BC，BE和CD相交于点F，且S△EFC=3S△EFD，求S△ADE：S△ABC的值．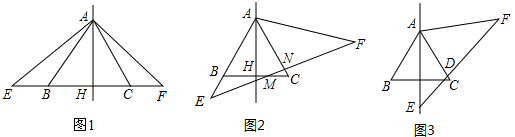
如图，已知?ABCD中，∠AEF=∠ACB，AD=kAC，试判断AE、EF的数量关系．