题目内容
7．
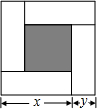如图，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个相同长方形的两边长（x＞y），给出以下关系式：①x+y=m；②x-y=n；③xy=$\frac{{m}^{2}-{n}^{2}}{4}$． 其中正确的关系式的个数有（ ）| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
分析 利用大正方形的边长=长方形的长+长方形的宽，小正方形的边长=长方形的长一长方形的宽，大正方形的面积一小正方形的面积=4个长方形的面积判定即可．
解答 解：由图形可得：①大正方形的边长=长方形的长+长方形的宽，故x+y=m正确；
②小正方形的边长=长方形的长一长方形的宽，故x-y=n正确；
③大正方形的面积一小正方形的面积=4个长方形的面积，故xy=$\frac{{m}^{2}-{n}^{2}}{4}$正确．
所以正确的个数为3．
故选：D．
点评 本题主要考查了平方差的几何背景，解题的关键是正确分析图形之间的边长及面积关系．
练习册系列答案
相关题目
如图，在△ABC中，∠CAB=90°，点D、E、F分别是BC、AC、AB的中点，连结EF，AD．求证：EF=AD．
18．已知$\frac{|x|}{x-2}$=$\frac{x}{2-x}$，则x一定满足（ ）
| A． | x＜2 | B． | x≤0 | C． | x≥0 | D． | x≥0且x≠2 |
2．
如图，若AD∥BC，那么（ ）
如图，若AD∥BC，那么（ ）| A． | ∠1=∠3 | B． | ∠2=∠4 | C． | ∠B=∠D | D． | ∠B=∠3 |
已知反比例函数y1=$\frac{k}{x}$和二次函数y2=-x2+bx+c的图象都过点A（-1，2）
如图，正方形ABCD的边长是5cm，以直线AB为轴，将正方形旋转一周，所得几何体的左视图的面积是50cm2 （结果保留π）．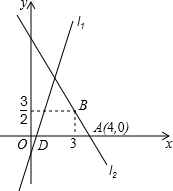
如图，直线l1的解析表达式为y=3x-3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．