题目内容
11.计算:(1)$\frac{1}{2}$$\sqrt{17}$-2$\sqrt{17}$;
(2)$\sqrt{\frac{1}{2}}$+$\sqrt{\frac{1}{8}}$;
(3)3$\sqrt{\frac{1}{3}}$+$\sqrt{12}$;
(4)$\sqrt{48}$+2$\sqrt{3}$-$\sqrt{75}$;
(5)($\sqrt{24}$-$\sqrt{6}$)÷2$\sqrt{3}$;
(6)$\frac{\sqrt{12}+\sqrt{27}}{\sqrt{3}}$;
(7)$\sqrt{3}$×$\sqrt{6}$$-\sqrt{20}$÷$\sqrt{5}$;
(8)$\sqrt{24}$-$\sqrt{18}$×$\sqrt{\frac{1}{3}}$$-\sqrt{\frac{1}{9}}$.
分析 (1)先化简,再计算即可;
(2)先化简,再计算即可;
(3)先化简,再计算即可;
(4)先化简,再计算即可;
(5)根据二次根式的除法法则计算;
(6)根据二次根式的除法法则计算;
(7)根据二次根式的乘除混合运算法则计算;
(8)先化简,再根据二次根式的乘除混合运算法则计算.
解答 解:(1)$\frac{1}{2}$$\sqrt{17}$-2$\sqrt{17}$=-$\frac{3}{2}\sqrt{17}$;
(2)$\sqrt{\frac{1}{2}}$+$\sqrt{\frac{1}{8}}$=$\frac{\sqrt{2}}{2}$+$\frac{\sqrt{2}}{4}$=$\frac{3\sqrt{2}}{4}$;
(3)3$\sqrt{\frac{1}{3}}$+$\sqrt{12}$=$\sqrt{3}$+2$\sqrt{3}$=3$\sqrt{3}$;
(4)$\sqrt{48}$+2$\sqrt{3}$-$\sqrt{75}$=4$\sqrt{3}$+2$\sqrt{3}$-5$\sqrt{3}$=$\sqrt{3}$;
(5)($\sqrt{24}$-$\sqrt{6}$)÷2$\sqrt{3}$=(2$\sqrt{6}$-$\sqrt{6}$)÷2$\sqrt{3}$=$\sqrt{6}$÷2$\sqrt{3}$=$\frac{\sqrt{2}}{2}$;
(6)$\frac{\sqrt{12}+\sqrt{27}}{\sqrt{3}}$=$\frac{\sqrt{12}}{\sqrt{3}}$+$\frac{\sqrt{27}}{\sqrt{3}}$=$\sqrt{4}$$+\sqrt{9}$=2+3=5;
(7)$\sqrt{3}$×$\sqrt{6}$$-\sqrt{20}$÷$\sqrt{5}$=3$\sqrt{2}$-2;
(8)$\sqrt{24}$-$\sqrt{18}$×$\sqrt{\frac{1}{3}}$$-\sqrt{\frac{1}{9}}$=2$\sqrt{6}$-$\sqrt{6}$$-\frac{1}{3}$=$\sqrt{6}$$-\frac{1}{3}$.
点评 本题考查的是二次根式的混合运算,掌握二次根式的化简、合并同类二次根式的法则以及二次根式的乘除法法则是解题的关键.

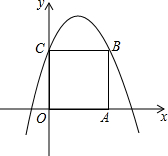 如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$.
如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$.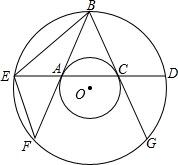 两个同心圆中,过大圆上一点B作大圆的弦BF,BG都和小圆相切,切点分别是A,C,经过点A,C作大圆的弦DE.
两个同心圆中,过大圆上一点B作大圆的弦BF,BG都和小圆相切,切点分别是A,C,经过点A,C作大圆的弦DE.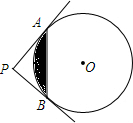 如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.
如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.