题目内容
8.如图所示,分别在三角形、四边形、五边形的广场各角修建半径为R的扇形草坪(图中阴影部分).(1)分别求图①②③中草坪的面积;
(2)如果多边形的边数为n,其余条件都不变,那么,你认为草坪的面积为多少?

分析 (1)求得三角形的内角和,求得四边形的内角和,求得五边形的内角和,然后利用扇形的面积公式即可求解;
(2)求得多边形的内角和,然后利用扇形的面积公式即可求解.
解答 解:(1)图①中三个角的和是:180°,则面积是:$\frac{180π{R}^{2}}{360}$=$\frac{1}{2}$πR2;
图②四个内角的和是:360°,则面积是:$\frac{360π{R}^{2}}{360}$=πR2;
图③五个内角的和是:540°,则面积是:$\frac{540π{R}^{2}}{360}$=$\frac{3}{2}$πR2;
(2)多边形边数为n,则内角和是:(n-2)•180°,则面积是:$\frac{(n-2)•180π{R}^{2}}{360}$=$\frac{n-2}{2}$πR2.
点评 本题考查了多边形的内角和以及扇形的面积公式,正确理解公式是关键.

练习册系列答案
相关题目
 如图,已知在四边形ABCD中,AE,BD于EE,CF,BD于F,AE=CF,BF=DE,求证:四边形ABCD是平行四边形.
如图,已知在四边形ABCD中,AE,BD于EE,CF,BD于F,AE=CF,BF=DE,求证:四边形ABCD是平行四边形.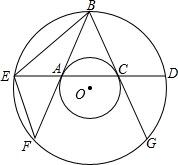 两个同心圆中,过大圆上一点B作大圆的弦BF,BG都和小圆相切,切点分别是A,C,经过点A,C作大圆的弦DE.
两个同心圆中,过大圆上一点B作大圆的弦BF,BG都和小圆相切,切点分别是A,C,经过点A,C作大圆的弦DE.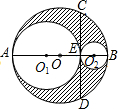 如图,AB是⊙O的直径,弦CD⊥AB于E,分别以AE、BE为直径作两个大小不同的⊙O1和⊙O2,若CD=16,则图中阴影部分的面积为32π(结果保留π).
如图,AB是⊙O的直径,弦CD⊥AB于E,分别以AE、BE为直径作两个大小不同的⊙O1和⊙O2,若CD=16,则图中阴影部分的面积为32π(结果保留π).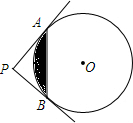 如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.
如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.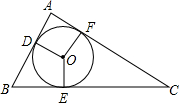 如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.
如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.