题目内容
15.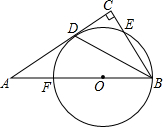 已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.
已知:点F在线段AB上,BF为⊙0的直径,点D在⊙O上,BC⊥AD于点C,BD平分∠ABC.(1)求证:AC是⊙0的切线;
(2)若AD=4,AF=2,求CD的长.
分析 (1)连接OD,证明OD⊥AC即可;
(2)连接DF,通过证得△ADF∽△ABD,求得AB=8,BF=6,$\frac{DF}{DB}$=$\frac{1}{2}$,根据勾股定理求得DF,DB,然后证得△BDF∽△BCD,即可求出CD的长.
解答 (1)证明:连接OD.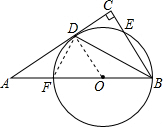
∵OD=OB,
∴∠OBD=∠ODB,
∵BD平分∠ABC,
∴∠OBD=∠DBC,
∴∠DBC=∠ODB,
∴OD∥BC,
∴∠ODA=∠C,
∵BC⊥AD,
∴OD⊥AC,
∴AC是⊙O的切线;
(2)解:连接DF,
∴AC是⊙0的切线,
∴AD2=AF•AB,
∵AD=4,AF=2,
∴AB=8,
∴BF=6,
∵△ADF∽△ABD,
∴$\frac{DF}{DB}$=$\frac{AD}{AB}$=$\frac{4}{8}$=$\frac{1}{2}$,
∴DB=2DF,
∵BF2=DB2+DF2,
∴62=4DF2+DF2,
∴DF=$\frac{6\sqrt{5}}{5}$,
∴DB=$\frac{12\sqrt{5}}{5}$,
∵BF为⊙0的直径,
∴∠BDF=90°,
∴∠BDF=∠C,
∵∠FBD=∠DBC,
∴△BDF∽△BCD,
∴$\frac{CD}{DF}$=$\frac{BD}{BF}$,即$\frac{CD}{\frac{6\sqrt{5}}{5}}$=$\frac{\frac{12\sqrt{5}}{5}}{6}$,
∴CD=$\frac{12}{5}$.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线,圆周角定理,勾股定理的运用以及三角形相似的判定和性质,具有一定的综合性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
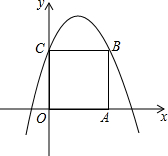 如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$.
如图,在平面直角坐标系中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,抛物线y=ax2+bx+c(a<0)经过B、C两点,则$\frac{b}{a}$的值为-$\frac{1}{2}$.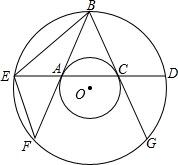 两个同心圆中,过大圆上一点B作大圆的弦BF,BG都和小圆相切,切点分别是A,C,经过点A,C作大圆的弦DE.
两个同心圆中,过大圆上一点B作大圆的弦BF,BG都和小圆相切,切点分别是A,C,经过点A,C作大圆的弦DE.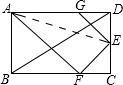 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处(AE为折痕,点E在CD上),在AD上截取DG,使以DG=CF.
如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处(AE为折痕,点E在CD上),在AD上截取DG,使以DG=CF.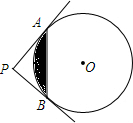 如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.
如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.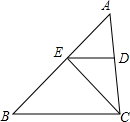 如图,∠AEC=70°,∠B=35°,EF平分∠AEC,试说明ED∥BC.
如图,∠AEC=70°,∠B=35°,EF平分∠AEC,试说明ED∥BC.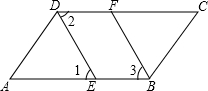 如图,如果∠1=∠3,可判定BF∥DE;如果∠1=∠2,可判定AB∥CD.
如图,如果∠1=∠3,可判定BF∥DE;如果∠1=∠2,可判定AB∥CD.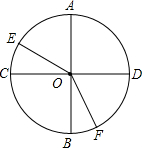 圆O的两条直径AB⊥CD,∠AOE=50°,∠DOF是∠BOF的2倍.
圆O的两条直径AB⊥CD,∠AOE=50°,∠DOF是∠BOF的2倍.