题目内容
9.设a,b为实数,已知A点是抛物线y=a(x-1)2+b与y轴的交点,B点是抛物线的顶点,过A,B的直线为y=2x+3,则a=-2,b=5.分析 根据抛物线的解析式求得A、B的坐标,代入y=2x+3得到关于a、b的方程组,解方程组即可求得.
解答 解:由抛物线y=a(x-1)2+b可知B(1,b),
令x=0,则y=a+b,
∴A(0,a+b),
∵过A,B的直线为y=2x+3,
∴$\left\{\begin{array}{l}{2+3=b}\\{3=a+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-2}\\{b=5}\end{array}\right.$.
故答案为-2,5.
点评 本题考查了二次函数的性质,求得A、B点的坐标是解题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
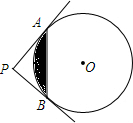 如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.
如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.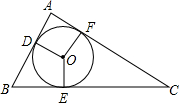 如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.
如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.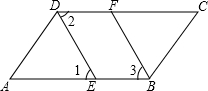 如图,如果∠1=∠3,可判定BF∥DE;如果∠1=∠2,可判定AB∥CD.
如图,如果∠1=∠3,可判定BF∥DE;如果∠1=∠2,可判定AB∥CD.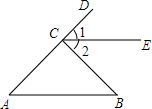 如图,已知∠A=∠B,点A,C,D在同一条直线上,∠DCB=∠A+∠B,CE是∠DCB的平分线,试说明CE∥AB.
如图,已知∠A=∠B,点A,C,D在同一条直线上,∠DCB=∠A+∠B,CE是∠DCB的平分线,试说明CE∥AB.
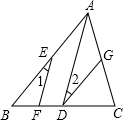 已知:如图,AD∥EF,∠1=∠2,判断AB与DG的位置关系,并说明理由.
已知:如图,AD∥EF,∠1=∠2,判断AB与DG的位置关系,并说明理由.