题目内容
10.如图1,在△ACB中,∠ACB=90°,AC=8,BC=6,正方形CDEF从点C出发沿射线CA匀速运动,当点C与点A重合时停止,正方形CDEF运动的速度为v,与△ABC重叠部分的面积为S,S关于运动时间t的部分图象如图2所示.(1)填空:CD=3,v=1.
(2)求S关于t的函数解析式,并写出t的取值范围;
(3)当S的值为6时,求出相应的t的值.
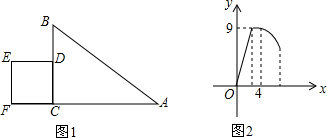
分析 (1)根据图中信息可以知道正方形EFCD的面积,即可求出边长,再根据速度=路程÷时间可以求出速度.
(2)分四种情形:①当0<x≤3时,②当3<x≤4时,③4<x≤7时,④当7<x≤8时,分别求出重合部分面积即可.
(3)利用(2)结论可以得到结论.
解答 解:(1)由图2可知:正方形EFCD的面积为9,所以CD=3,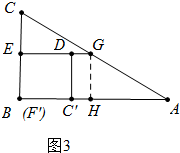
在如图3中,延长ED交AC于G,作GH⊥AB于H,则四边形EGHB是矩形,
∵EG∥AB,
∴$\frac{EG}{AB}$=$\frac{CE}{CB}$,
∴$\frac{EG}{8}$=$\frac{3}{6}$,
∴EG=4,
∴BH=EG=4,
∴V=$\frac{BH}{4}$=1,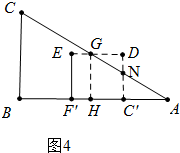
故答案为3,1.
(2)①当0<x≤3时,s=3t.
②当3<x≤4时,s=9.
③4<x≤7时,如图4中,
s=S正方形EFCD-S△DGN=9-$\frac{1}{2}$•[3-$\frac{3}{4}$(8-t)]•$\frac{4}{3}$[3-$\frac{3}{4}$(8-t)]=-$\frac{2}{3}$($\frac{3}{4}$t-3)2+9.
④当7<x≤8时,如图5中,
s=S△AGF′=$\frac{1}{2}$•(11-t)•$\frac{3}{4}$(11-t)=$\frac{3}{8}$(11-t)2.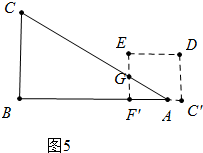 综上所述s=t$\left\{\begin{array}{l}{3t}&{(0<t≤3)}\\{9}&{(3<t≤4)}\\{-\frac{2}{3}(\frac{3}{4}t-3)^{2}+9}&{(4<t≤7)}\\{\frac{3}{8}(11-t)^{2}}&{(7<t≤8)}\end{array}\right.$.
综上所述s=t$\left\{\begin{array}{l}{3t}&{(0<t≤3)}\\{9}&{(3<t≤4)}\\{-\frac{2}{3}(\frac{3}{4}t-3)^{2}+9}&{(4<t≤7)}\\{\frac{3}{8}(11-t)^{2}}&{(7<t≤8)}\end{array}\right.$.
(3)s=6时,3t=6,t=2,
或-$\frac{2}{3}$($\frac{3}{4}$x-3)2+9=6,
t=4+2$\sqrt{2}$或4-2$\sqrt{2}$舍弃.
∴t=2或4+2$\sqrt{2}$时s的值为6.
点评 本题考查动点问题,正方形的性质、勾股定理等知识,解题的关键是读懂题意,学会分类讨论的思想,属于中考常考题型.

 同步练习强化拓展系列答案
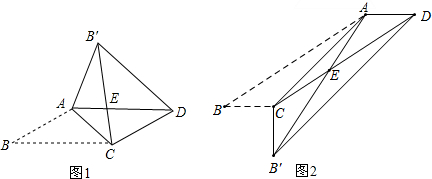
同步练习强化拓展系列答案 如图,已知在四边形ABCD中,AE,BD于EE,CF,BD于F,AE=CF,BF=DE,求证:四边形ABCD是平行四边形.
如图,已知在四边形ABCD中,AE,BD于EE,CF,BD于F,AE=CF,BF=DE,求证:四边形ABCD是平行四边形.
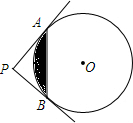 如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.
如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.