题目内容
12.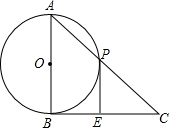 已知:如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点P,点E在BC上,并且PE切⊙O于点P.求证:CE=BE.
已知:如图,AB为⊙O的直径,BC切⊙O于点B,AC交⊙O于点P,点E在BC上,并且PE切⊙O于点P.求证:CE=BE.
分析 连接PB,根据切线的性质,就可以证出∠C=∠CPE,从而证明BE=CE.
解答 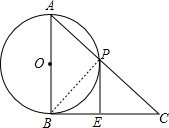 证明:连接PB,
证明:连接PB,
∵∠ABC=90°,AB为⊙O直径,
∵BC为⊙O切线,且∠ABC=90°,
∵PE切⊙O于点P,
∴BE=PE,
∴∠PBE=∠BPE,
∵∠C+∠CBP=∠CPE+∠EPB=90°,
∴∠C=∠CPE,
∴CE=EP,
∴BE=CE.
点评 本题主要考查了切线的性质定理,以及等腰三角形的判定定理,连接PB构造直角三角形是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.已知$\sqrt{x}$=6.5012,650.12=$\sqrt{422630}$,则x=( )
| A. | 4226.3 | B. | 42.263 | C. | 0.042263 | D. | 42263000 |
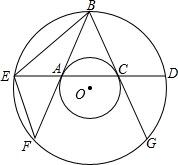 两个同心圆中,过大圆上一点B作大圆的弦BF,BG都和小圆相切,切点分别是A,C,经过点A,C作大圆的弦DE.
两个同心圆中,过大圆上一点B作大圆的弦BF,BG都和小圆相切,切点分别是A,C,经过点A,C作大圆的弦DE.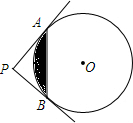 如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.
如图,PA,PB切⊙O于点A,B,PA⊥PB于点P,若PA=4,求图中阴影部分的面积.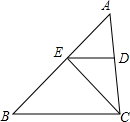 如图,∠AEC=70°,∠B=35°,EF平分∠AEC,试说明ED∥BC.
如图,∠AEC=70°,∠B=35°,EF平分∠AEC,试说明ED∥BC.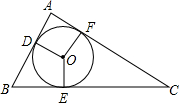 如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.
如图,⊙O是△ABC的内切圆,与AB、BC、CA分别相切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的大小.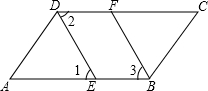 如图,如果∠1=∠3,可判定BF∥DE;如果∠1=∠2,可判定AB∥CD.
如图,如果∠1=∠3,可判定BF∥DE;如果∠1=∠2,可判定AB∥CD.