题目内容
17.一艘船沿江从A港顺流行驶到B港,比从B港返回A港少用2小时.若轮船在静水中的速度为30千米/时,水速为2千米/时,求A港和B港相距多少千米?分析 根据逆流速度=静水速度-水流速度,顺流速度=静水速度+水流速度,表示出逆流速度与顺流速度,根据题意列出方程,求出方程的解即可得到结果.
解答 解:设A港和B港相距x千米,
可得方程:$\frac{x}{30-2}$-2=$\frac{x}{30+2}$,
解得x=448.
答:A港和B港相距448千米.
点评 此题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
12.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.

(1)根据图中提供的信息填表:
则S=$\frac{1}{2}$m+n-1(用含m、n的代数式表示)
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=m+2(n-1)(用含m、n的代数式表示).


(1)根据图中提供的信息填表:
| 格点多边形各边上的 格点的个数 | 格点边多边形内部的 格点个数 | 格点多边形的面积 | |
| 多边形1 | 4 | 1 | 2 |
| 多边形2 | 5 | 2 | ②$\frac{7}{2}$ |
| 多边形3 | 6 | 3 | 5 |
| 多边形4 | ①5 | 4 | $\frac{11}{2}$ |
| 一般格点多边形 | m | n | S |
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=m+2(n-1)(用含m、n的代数式表示).

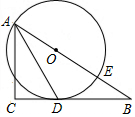 如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD. 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,求BD的长.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,求BD的长. 如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,BA,ED的延长线交于点F.
如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,BA,ED的延长线交于点F.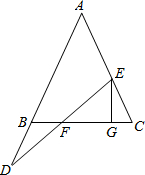 如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.