题目内容
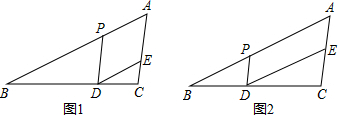
11.如图1,△ABC中,点P在AB边上自点A向终点B运动,运动速度为每秒1个单位长度,过点P作PD∥AC,交BC于点D,过D点作DE∥AB,交AC于点E,且AB=10,AC=5,设点P运动的时间为t秒(0<t<10).(1)填空:当 t=5秒时,△PBD≌△EDC;
(2)当四边形APDE是菱形时.试求t的值?
(3)如图2,若△ABC的面积为20,四边形APDE的面积为S,试问S是否有最大值?如果有最大值,请求出最大值,如果没有请说明理由.
分析 (1)先判断出四边形APDE是平行四边形,得出DE=AP,再由全等三角形的性质建立方程求解即可;
(2)先判断出△CDE∽△CBA,得出CE=$\frac{1}{2}$t,再利用菱形的性质得出AP=AE,建立方程求解即可;
(3)借助(2)得出△CDE∽△CBA,利用相似三角形的面积比等于相似比的平方得出S△CED=$\frac{{t}^{2}}{5}$,同理得出S△DPB=$\frac{(10-t)^{2}}{5}$,最后用面积的差得出S=-$\frac{2}{5}$(t-5)2+10(0<t<10),即可确定出结论.
解答 解:(1)由运动知,AP=t,
∵AB=10,
∴BP=10-t,
∵DP∥AC,DE∥AB,
∴四边形APDE是平行四边形,
∴DE=AP,
∵△PBD≌△EDC,
∴BP=DE,
∴BP=AP,
∴t=10-t,
∴t=5,
故答案为5;
(2)由(1)知,AP=DE=t,
∵DE∥AB,
∴△CDE∽△CBA,
∴$\frac{DE}{AB}=\frac{CE}{AC}$,
∵AB=10,AC=5,
∴CE=$\frac{1}{2}$t,
∴AE=AC-CE=5-$\frac{1}{2}$t,
∵四边形APDE是菱形,
∴AP=AE,
∴t=5-$\frac{1}{2}$t,
∴t=$\frac{10}{3}$;
(3)S有最大值,理由如下:
∵DE∥AB,
∴△CDE∽△CBA,
∴$\frac{{S}_{△CED}}{{S}_{△CAB}}=(\frac{ED}{AB})^{2}$=$(\frac{t}{10})^{2}$=$\frac{{t}^{2}}{100}$,
∵S△CAB=20,
∴S△CED=$\frac{{t}^{2}}{100}$×S△CAB=$\frac{{t}^{2}}{5}$,
同理:S△DPB=$\frac{(10-t)^{2}}{5}$,
∴S=S△CAB-S△CED-S△DPB
=20-$\frac{{t}^{2}}{5}$-$\frac{(10-t)^{2}}{5}$
=-$\frac{2}{5}$(t-5)2+10(0<t<10)
当t=5时,S最大=10.
即:S有最大值,最大值为10.
点评 此题是四边形综合题,主要考查了平行四边形的判定和性质,相似三角形的判定和性质,全等三角形的性质,菱形的性质,解(2)的关键是得出AE=5-$\frac{1}{2}$t,解(3)的关键是利用相似三角形的想得出S△CED=$\frac{{t}^{2}}{5}$,S△DPB=$\frac{(10-t)^{2}}{5}$,本题体现了方程的思想,属于中考压轴题.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案(1)请你在下表的空格里填写适当的代数式:
| 排数 | 第1排 | 第2排 | 第3排 | 第4排 | … | 第n排 |
| 座位数 | 24 | 24+a | 24+2a | 24+3a | … | 24+(n-1)a |
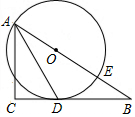 如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD. 二次函数y=ax2+bx+c(a≠0)的图象如图(虚线部分为对称轴),给出以下5个结论:①x≤1时,y随x的增大而增大;②abc>0;③b<a+c;④4a+2b+c>0;⑤3a-b<0,其中正确的结论有①④⑤(填上所有正确结论的序号).
二次函数y=ax2+bx+c(a≠0)的图象如图(虚线部分为对称轴),给出以下5个结论:①x≤1时,y随x的增大而增大;②abc>0;③b<a+c;④4a+2b+c>0;⑤3a-b<0,其中正确的结论有①④⑤(填上所有正确结论的序号). 已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E.
已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E.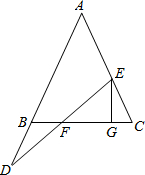 如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.