题目内容
16.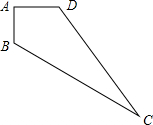 如图所示,在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=13,CD=12.试求四边形ABCD的面积.
如图所示,在四边形ABCD中,∠A=90°,AB=3,AD=4,BC=13,CD=12.试求四边形ABCD的面积.
分析 先根据勾股定理求出BD的长度,再根据勾股定理的逆定理判断出△BCD的形状,再利用三角形的面积公式求解即可.
解答 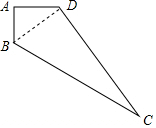 解:连接BD,
解:连接BD,
∵∠A=90°,AB=3,AD=4,
∴BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{9+16}$=5,
在△BCD中,
BD2+DC2=25+144=169=CB2,
∴△BCD是直角三角形,
∴S四边形ABCD=$\frac{1}{2}$AB•AD+$\frac{1}{2}$BD•BC,
=$\frac{1}{2}$×3×4+$\frac{1}{2}$×5×12,
=36.
答:四边形ABCD的面积是36.
点评 本题考查的是勾股定理的逆定理及三角形的面积,能根据勾股定理的逆定理判断出△BCD的形状是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
18.数轴上表示6的点,移动2个单位后,这个点表示的数是( )
| A. | 4或-4 | B. | 8 | C. | -4 | D. | 4或8 |
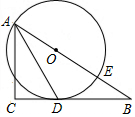 如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD. 已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E.
已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E. 数学活动课上,同学们正在讨论一道习题:
数学活动课上,同学们正在讨论一道习题: 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,求BD的长.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,求BD的长.