题目内容
20.如图,O是直线AB上一点,∠COD是直角,OE是∠BOC的平分线.(1)如图1,若∠AOC=40°,求∠DOE的度数;
(2)在图1中,若∠AOC=α,直接写出∠DOE的度数(用含α的代数式表示);
(3)将图1中的∠COD按顺时针方向旋转至图2所示的位置.探究∠AOC与∠DOE之间的数量关系,写出你的结论,并说明理由;

分析 (1)先根据邻补角定义求出∠BOC,根据角平分线定义求出∠COE,代入∠DOE=∠COD-∠COE求出即可;
(2)先根据邻补角定义求出∠BOC,根据角平分线定义求出∠COE,代入∠DOE=∠COD-∠COE求出即可;
(3)先根据邻补角定义求出∠BOC,根据角平分线定义求出∠COE,代入∠DOE=∠COD-∠COE求出即可.
解答 解:(1)∵O是直线AB上一点(如图1),
∴∠AOC+∠BOC=180°.
∵∠AOC=40°,
∴∠BOC=140°.
∵OE平分∠BOC,
∴∠COE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×140°=70°.
∵∠DOE=∠COD-∠COE,∠COD=90°,
∴∠DOE=20°;
(2)∠DOE=$\frac{1}{2}$α,
理由是:∵O是直线AB上一点(如图1),
∴∠AOC+∠BOC=180°.
∵∠AOC=α,
∴∠BOC=180°-α.
∵OE平分∠BOC,
∴∠COE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×(180°-α)=90°-$\frac{1}{2}α$,
∵∠DOE=∠COD-∠COE,∠COD=90°,
∴∠DOE=$\frac{1}{2}$α;
(3)∠DOE=$\frac{1}{2}$∠AOC.
理由如下:
∵O是直线AB上一点(如图2),
∴∠AOC+∠BOC=180°.
∴∠BOC=180°-∠AOC.
∵OE平分∠BOC,
∴∠COE=$\frac{1}{2}$∠BOC=$\frac{1}{2}$(180°-∠AOC),
∵∠DOE=∠COD-∠COE,∠COD=90°,
∴∠DOE=90°-$\frac{1}{2}$(180°-∠AOC)=$\frac{1}{2}$∠AOC,
∴∠DOE=$\frac{1}{2}$∠AOC.
点评 本题考查了角平分线定义,角的有关计算等知识点,能正确求出∠COE的度数是解此题的关键,求解过程类似.


(1)根据图中提供的信息填表:
| 格点多边形各边上的 格点的个数 | 格点边多边形内部的 格点个数 | 格点多边形的面积 | |
| 多边形1 | 4 | 1 | 2 |
| 多边形2 | 5 | 2 | ②$\frac{7}{2}$ |
| 多边形3 | 6 | 3 | 5 |
| 多边形4 | ①5 | 4 | $\frac{11}{2}$ |
| 一般格点多边形 | m | n | S |
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=m+2(n-1)(用含m、n的代数式表示).

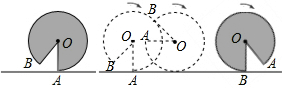
| A. | 10πcm | B. | 20πcm | C. | 24πcm | D. | 30πcm |
 已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E.
已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E. 如图,在⊙O中,AB,BC为互相垂直且相等的两条弦,连接AC.求证:
如图,在⊙O中,AB,BC为互相垂直且相等的两条弦,连接AC.求证: 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,求BD的长.
如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=$5\sqrt{5}$,求BD的长.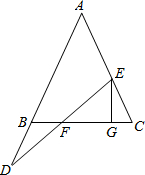 如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
如图,在△ABC中,AB=AC,点E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.