题目内容
11．已知关于x的方程x2-3x+k=0．（1）当k为何值时，方程有两个不相等的实数根？
（2）当k为何值时，方程有两个相等的实数根？
（3）当k为何值时，方程没有实数根？
分析 先求出△，（1）由△＞0，解关于k不等式求出k的范围；（2）由△=0，解关于k的方程求出的值；（3）由△＜0，解关于k的不等式求出k的范围．
解答 解：△=（-3）2-4×1×k=9-4k，
（1）当△＞0，方程有两个不相等的实数根；
即9-4k＞0，所以k＜$\frac{9}{4}$；
（2）当△=0，方程有两个相等的实数根；
即9-4k=0，所以k=$\frac{9}{4}$；
（3）当△＜0，方程没有实数根；
即9-4k＜0，所以k＞$\frac{9}{4}$．
点评 本题考查了一元二次方程ax2+bx+c=0（a≠0，a，b，c为常数）根的判别式．当△＞0，方程有两个不相等的实数根；当△=0，方程有两个相等的实数根；当△＜0，方程没有实数根．同时考查了不等式的解法．
练习册系列答案
相关题目
1．已知y=2x，z=$\frac{1}{y}$，那么z与x之间的关系是（ ）
| A． | 成正比例 | B． | 成反比例 | ||
| C． | 有可能成正比例有可能成反比例 | D． | 无法确定 |
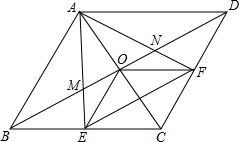如图，在菱形ABCD中，对角线AC与BD相交于点O，∠ABC=60°，点E，F分别是BC，CD的中点，BD分别与AE，AF相交于点M，N，连接OE，OF，下列结论：（1）△AEF是等边三角形；（2）四边形CEOF是菱形；（3）OF⊥AE；（4）BM=MN=ND．其中正确的结论有（ ）
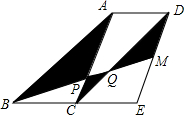如图，四边形ABCD和四边形ACED都是平行四边形，点M为DE的中点，BM分别交AC和CD于点P，Q．若△ABC的面积为6，则图中阴影部分的面积为7．