题目内容
1. 如图,Rt△ABC中,∠C=90°,∠B=2∠A,CD⊥AB于D,则$\frac{AD}{BD}$=3.
如图,Rt△ABC中,∠C=90°,∠B=2∠A,CD⊥AB于D,则$\frac{AD}{BD}$=3.
分析 由∠C=90°,∠B=2∠A,得到∠A=30°,∠B=60°,根据CD⊥AB于D,求得∠CDB=90°,于是得到∠BCD=30°,设BD=k,根据直角三角形的性质得到BC=2k,AB=4k,求出AD=AB=BD=3k,即可得到结论.
解答 解:∵∠C=90°,∠B=2∠A
∴∠A=30°,∠B=60°,
∵CD⊥AB于D,
∴∠CDB=90°,
∴∠BCD=30°,
设BD=k,
∴BC=2k,AB=4k,
∴AD=AB=BD=3k,
∴$\frac{AD}{BD}$=$\frac{3k}{k}$=3.
故答案为:3.
点评 本题主要考查了直角三角形30°角所对的直角边等于斜边的一半的性质,同角的余角相等的性质,熟记性质是解题的关键.

练习册系列答案
相关题目
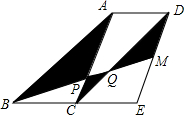 如图,四边形ABCD和四边形ACED都是平行四边形,点M为DE的中点,BM分别交AC和CD于点P,Q.若△ABC的面积为6,则图中阴影部分的面积为7.
如图,四边形ABCD和四边形ACED都是平行四边形,点M为DE的中点,BM分别交AC和CD于点P,Q.若△ABC的面积为6,则图中阴影部分的面积为7. 如图,△ABC中,D是AB中点,E是AC上的点,且3AE=2AC,CD,BE交于O点,求证:OE=$\frac{1}{4}$BE.
如图,△ABC中,D是AB中点,E是AC上的点,且3AE=2AC,CD,BE交于O点,求证:OE=$\frac{1}{4}$BE.