题目内容
14.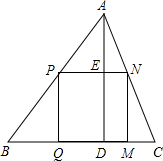 △ABC是一块锐角三角形余料,边BC=180mm,高AD=120mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.
△ABC是一块锐角三角形余料,边BC=180mm,高AD=120mm,要把它加工成矩形零件,使一边在BC上,其余两个顶点分别在边AB、AC上.(1)若这个矩形是正方形,那么边长是多少?
(2)若这个矩形的长是宽的2倍,则边长是多少?
分析 (1)设出边长为xmm,由正方形的性质得出PN∥BC,PQ∥AD,根据平行线的性质,可以得出比例关系式,$\frac{PQ}{AD}$=$\frac{BP}{AB}$、$\frac{PN}{BC}$=$\frac{AP}{AB}$,代入数据求解即可.
(2)设宽为xmm,则长为2xmm,同(1)列出比例关系求解,但是要注意有两种情况,PQ可以为长也可以为宽,分两种情况分别求解即可.
解答 解:(1)设边长为xmm,
∵矩形为正方形,
∴PN∥BC,PQ∥AD,
根据平行线的性质可以得出:$\frac{PQ}{AD}$=$\frac{BP}{AB}$、$\frac{PN}{BC}$=$\frac{AP}{AB}$,
由题意知PQ=x,BC=180mm,AD=120mm,PN=x,
即$\frac{x}{120}$=$\frac{BP}{AB}$,$\frac{x}{180}$=$\frac{AP}{AB}$,
∵AP+BP=AB,
∴$\frac{x}{120}$+$\frac{x}{180}$=$\frac{BP}{AB}$+$\frac{AP}{AB}$=1,
解得x=72.
答:若这个矩形是正方形,那么边长是72mm.
(2)设边宽为xmm,则长为2xmm,
∵四边形PNMQ为矩形,
∴PN∥BC,PQ∥AD,
根据平行线的性质可以得出:$\frac{PQ}{AD}$=$\frac{BP}{AB}$、$\frac{PN}{BC}$=$\frac{AP}{AB}$,
①PQ为长,PN为宽:
由题意知PQ=2xmm,AD=120mm,BC=180mm,AN=xmm,
即$\frac{2x}{120}$=$\frac{BP}{AB}$,$\frac{x}{180}$=$\frac{AP}{AB}$,
∵AP+BP=AB,
∴$\frac{2x}{120}$+$\frac{x}{180}$=$\frac{BP}{AB}$+$\frac{AP}{AB}$=1,
解得x=45,2x=90.
即长为90mm,宽为45mm.
②PQ为宽,PN为长:
由题意知PQ=xmm,AD=120mm,BC=180mm,PN=2xmm,
即$\frac{x}{120}$=$\frac{BP}{AB}$,$\frac{2x}{180}$=$\frac{AP}{AB}$,
∵AP+BP=AB,
∴$\frac{x}{120}$+$\frac{2x}{180}$=$\frac{BP}{AB}$+$\frac{AP}{AB}$=1,
解得x=$\frac{360}{7}$,2x=$\frac{720}{7}$.
即长为$\frac{720}{7}$mm,宽为$\frac{360}{7}$mm.
答:矩形的长为90mm,宽是45mm或者长为$\frac{720}{7}$mm,宽为$\frac{360}{7}$mm.
点评 本题考查了相似三角形的应用,主要利用了相似三角形对应高的比等于相似比,熟记性质并列出比例式是解题的关键.

 如图,已知直线a,b交于点O,∠1+∠2=218°,则∠1=109°,∠2=109°,∠3=71°.
如图,已知直线a,b交于点O,∠1+∠2=218°,则∠1=109°,∠2=109°,∠3=71°.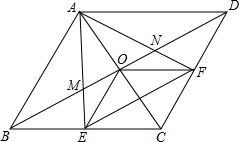 如图,在菱形ABCD中,对角线AC与BD相交于点O,∠ABC=60°,点E,F分别是BC,CD的中点,BD分别与AE,AF相交于点M,N,连接OE,OF,下列结论:(1)△AEF是等边三角形;(2)四边形CEOF是菱形;(3)OF⊥AE;(4)BM=MN=ND.其中正确的结论有( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,∠ABC=60°,点E,F分别是BC,CD的中点,BD分别与AE,AF相交于点M,N,连接OE,OF,下列结论:(1)△AEF是等边三角形;(2)四边形CEOF是菱形;(3)OF⊥AE;(4)BM=MN=ND.其中正确的结论有( )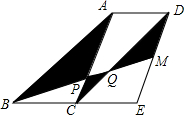 如图,四边形ABCD和四边形ACED都是平行四边形,点M为DE的中点,BM分别交AC和CD于点P,Q.若△ABC的面积为6,则图中阴影部分的面积为7.
如图,四边形ABCD和四边形ACED都是平行四边形,点M为DE的中点,BM分别交AC和CD于点P,Q.若△ABC的面积为6,则图中阴影部分的面积为7. 己知a,b,c在数轴上的位置如图所示.
己知a,b,c在数轴上的位置如图所示.