题目内容
4.解方程:(1)$\frac{2}{x+1}$=$\frac{x}{x-1}$-1;
(2)$\frac{2}{x+1}$-$\frac{x}{{x}^{2}-1}$=0.
分析 (1)先把方程两边乘以(x+1)(x-1),得到整式方程2(x-1)=x(x+1)-(x+1)(x-1),再解整式方程得x=3,然后进行检验确定原方程的解;
(2)先把方程两边乘以(x+1)(x-1),得到整式方程2(x-1)-x=0,再解整式方程得x=2,然后进行检验确定原方程的解.
解答 解:(1)去分母得2(x-1)=x(x+1)-(x+1)(x-1),
解得x=3,
检验:x=3时,(x+1)(x-1)≠0,所以x=3是原方程的解,
所以原方程的解为x=3;
(2)去分母得2(x-1)-x=0,
解得x=2,
检验:x=2时,(x+1)(x-1)≠0,所以x=2是原方程的解,
所以原方程的解为x=2.
点评 本题考查了解分式方程:解分式方程的步骤:去分母、求出整式方程的解、检验、结论.解分式方程时,一定要检验.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在同一平面直角坐标系内,将函数y=x-3的图象向右平移2个单位,再向下平移1个单位得到的图象与x轴的交点坐标是( )
| A. | (-6,0) | B. | (2,0) | C. | (6,0) | D. | (-1,0) |
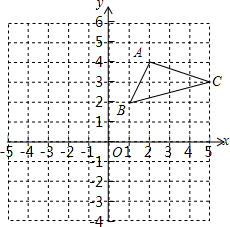 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4).