题目内容
15.在Rt△ABC中,∠C=90°,点G是重心,如果sinA=$\frac{1}{3}$,BC=2,那么GC的长等于2.分析 根据题意画出图形,根据sinA=$\frac{1}{3}$,BC=2可得出AB=3BC=6,利用直角三角形的性质求出CE的长,根据三角形重心的性质即可得出结论.
解答  解:如图所示,
解:如图所示,
∵在Rt△ABC中,∠C=90°,sinA=$\frac{1}{3}$,BC=2,
∴AB=3BC=6.
∵点G是重心,
∴CD为△ABC的中线,
∴CD=$\frac{1}{2}$AB=3,
∴CG=$\frac{2}{3}$CD=$\frac{2}{3}$×3=2.
故答案为:2.
点评 本题考查的是三角形的重心,根据题意画出图形,由锐角三角函数的定义求出AB的长是解答此题的关键.

练习册系列答案
相关题目
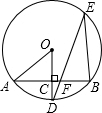 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在☉O上.
如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在☉O上.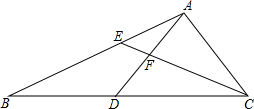 已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.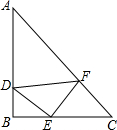 如图,△ABC,△DEF都是等腰直角三角形,D、E、F分别在AB、BC、CA上,已知∠B=∠DEF=90°,AB=BC,DE=EF.
如图,△ABC,△DEF都是等腰直角三角形,D、E、F分别在AB、BC、CA上,已知∠B=∠DEF=90°,AB=BC,DE=EF.