题目内容
19.请写出一个形状与抛物线y=2x2+x-1相同,并且经过原点的抛物线的函数表达式:y=2x2-2x.分析 设抛物线的解析式为y=ax2+bx,由条件可以得出a=2或-2,再将(0,0)代入解析式就可以求出结论.
解答 解:设抛物线的解析式为y=ax2+bx,且该抛物线的形状和抛物线y=2x2+x-1相同,
∴a=-2或2,
∴y=2x2-2x.
故答案为:y=-2x2-2x(答案不唯一).
点评 本题考查了二次函数的性质,运用抛物线的性质求出a值是解题的关健.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
9.若x=-27是-$\frac{1}{3}x$-m=4的解,则m的值是( )
| A. | -5 | B. | -13 | C. | 13 | D. | 5 |
8. 某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为200人,表中m的值为90;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
 某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).
某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成了不完整的表格和扇形统计图(如图).| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
| 频数 | 50 | m | 40 | 20 |
(1)本次问卷调查共抽取的学生数为200人,表中m的值为90;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?
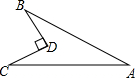 如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积.
如图所示,四边形ABDC,BD⊥CD,BD=6,CD=8,AB=24,AC=26,求该四边形的面积. 将两块直角三角尺的直角顶点重合为如图的位置,若∠AOC=20°,则∠BOD=20°.
将两块直角三角尺的直角顶点重合为如图的位置,若∠AOC=20°,则∠BOD=20°.