题目内容
如图，数轴上有A、B、C、D四个整数点（即各点均表示整数），且3AB=BC=2CD．若A、D两点所表示的数分别是﹣6和5，则线段AC的中点所表示的数是（ ）
A. ﹣3 B. ﹣1 C. 3 D. ﹣2
D
【解析】首先设BC为6x，根据3AB=BC=2CD表示出AB=2x，CD=3x，然后根据线段AD的长度建立方程，进而求出点C所表示的数，再利用两点之间的中点公式即可得出答案．
【解析】
设BC=6x，
∵3AB=BC=2CD，
∴AB=2x，CD=3x，
∴AD=AB+BC+CD=11x，
∵A，D两点所表示的数分别是?6和5，
∴AD=11，
...
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
已知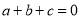
， 
.
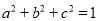（1）求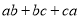
的值；
（2）求
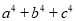的值．
（1） （2）
【解析】试题分析：（1）把a+b+c=0两边平方，然后利用代入法等量代换即可；
（2）把ab+bc+ca与两边分别乘方即可.
试题解析：（1）因为a+b+c=0
所以+2ab+2ac+2bc=0
∴2ab+2ac+2bc=-1
即ab+bc+ca=-
（2）因为a+b+c=0，a2+b2+c2=1
所以+2ab+2ac+2bc=0
... 如果(2x＋m)(x－5)展开后的结果中不含x的一次项，那么m等于( )
A. 5 B. －10 C. －5 D. 10
D
【解析】(2x＋m)(x－5)=2x2+mx-10x-5m，因展开后的结果中不含x的一次项，可得m-10=0，解得m=10，故选D. 如图，已知三角形ABC中有正方形EDFC，请你简述三角形AED到三角形PFD的变化过程是：_____________________________________
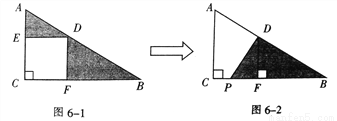
以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD
【解析】试题分析：由图可知三角形AED到三角形PFD，点D位置不变，点A至点P，点E至点F，AD＝PD，ED＝FD，根据旋转的性质可知：以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD．
故答案为：以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD． 用“●”“■”“”分别表示三种不同的物体，如图所示，前两架天平保持平衡，若要使第三架天平也平衡，那么“？”处应放“■”的个数为（ ）
A．2个 B．3个 C．4个 D．5个
D
【解析】
试题分析：设“●”“■”“”分别为x、y、z，由图可知，
，解得x=2y，z=3y，
所以x+z=2y+3y=5y，即“■”的个数为5，
故选D． 计算：（-3）+4的结果等于（ ）
A. +7 B. -7 C. 1 D. -1
C
【解析】试题分析：原式＝＋(4－3)＝1．
故选C． 观察下列运算并填空．
；
；
； 
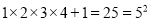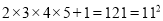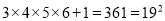根据以上结果，猜想并研究：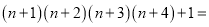 
__________．
【解析】试题解析：
…
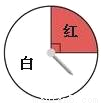
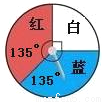
故答案为： . 下面是两个可以自由转动的转盘，转动转盘，分别计算转盘停止后，指针落在红色区域的概率.
【解析】分析：本题考察对概率意义的理解，关键是根据图示，由圆心角的度数求出概率.
本题解析:
由图可以看出，在第一个转盘内，红色区域的圆心角是90°，因此可以算得指针落在红色区域的概率是；在第二个转盘内，红色区域的圆心角是135°，因此可以算得指针落在红色区域的概率是 . 在Rt△ABC中，∠C=90°，cosB=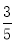
，AB=10cm，则BC的长度为( )
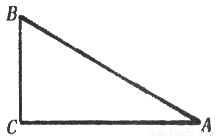
A. 6cm B. 7cm
C. 8cm D. 9cm
A
【解析】
试题分析：根据cosB=0.6可得：，则BC=6cm.