题目内容
如图,已知三角形ABC中有正方形EDFC,请你简述三角形AED到三角形PFD的变化过程是:_____________________________________
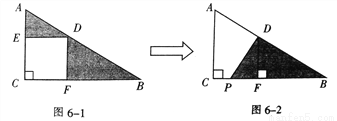
 以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD
【解析】试题分析:由图可知三角形AED到三角形PFD,点D位置不变,点A至点P,点E至点F,AD=PD,ED=FD,根据旋转的性质可知:以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD.
故答案为:以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD.
以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD
【解析】试题分析:由图可知三角形AED到三角形PFD,点D位置不变,点A至点P,点E至点F,AD=PD,ED=FD,根据旋转的性质可知:以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD.
故答案为:以点D为旋转中心将三角形AED按逆时针方向旋转90度后得三角形PFD.
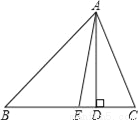
如图,已知△ABC中,AD是BC边上的高,点E在线段BD上,且AE平分∠BAC,若∠B=40°,∠C=78°,则∠EAD=__°.
 19
【解析】试题分析:根据三角形内角和定理称求得∠BAC,再由AE平分∠BAC,可求得∠EAC,最后由∠ADC=90°,∠C=78°,可求得∠DAC,即∠EAD可求.
19
【解析】试题分析:根据三角形内角和定理称求得∠BAC,再由AE平分∠BAC,可求得∠EAC,最后由∠ADC=90°,∠C=78°,可求得∠DAC,即∠EAD可求. 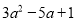 与
与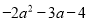 的和为 ( )
的和为 ( )
A. 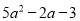 B.
B. 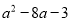 C.
C. 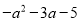 D.
D. 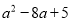
 B
【解析】由题意可得: +=,故选B.
B
【解析】由题意可得: +=,故选B. 数学课上,刘老师和学生做一个猜数游戏,他让学生按照以下步骤进行计算:
①任想一个两位数a,把a乘以2,再加上9,把所得的和再乘以2;
②把a乘以2,再加上30,把所得的和除以2;
③把①所得的结果减去②所得的结果,这个差即为最后的结果.
刘老师说:只要你告诉我最后的结果,我就能猜出你最初想的两位数a是多少.
这时学生小华计算的结果是69,刘老师立即猜出周晓晓最初想的两位数是22.
(1)用含a的代数式表示:步骤①的结果是 步骤②的结果是 步骤③的结果是
(2)若小强按这个猜数游戏的步骤计算后,说出的最后的结果是150,那么小强最初想的两位数是多少?
 (1)4a+18 a+15 3a+3(2)49
【解析】试题分析:(1)根据①②③步骤列出代数式,化简后即可得出结论;
(2)结合(1)可知3a+3=150,解之即可得出结论.
试题解析:
【解析】
(1)由题意可知,第①步运算的结果为:2(2a+9)=4a+18;
第②步运算的结果为: (2a+30)=a+15;
第③步运算的为:(4a+18)-(a+15)...
(1)4a+18 a+15 3a+3(2)49
【解析】试题分析:(1)根据①②③步骤列出代数式,化简后即可得出结论;
(2)结合(1)可知3a+3=150,解之即可得出结论.
试题解析:
【解析】
(1)由题意可知,第①步运算的结果为:2(2a+9)=4a+18;
第②步运算的结果为: (2a+30)=a+15;
第③步运算的为:(4a+18)-(a+15)... 如图OA⊥OC , OB⊥OD , 4位同学观察图形后分别说了自己的观点。
甲:∠AOB=∠COD; 乙:∠BOC+∠AOD = 1800;
丙:∠AOB+∠COD = 900; 丁:图中小于平角的角有5个;
其中正确的结论有( )
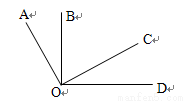
A.1个 B. 2个 C.3个 D.4个
 B
【解析】根据同角的余角相等可得,∠AOB=∠COD,而不会得出∠AOB+∠COD=90°,故甲正确,丙错误;∠BOC+∠AOD=∠BOC+∠AOB+∠BOD=∠AOC+∠BOD=90°+90°=180°,故乙正确;
图中小于平角的角有∠COD,∠BOD,∠AOD,∠BOC,∠AOC,∠AOB六个,故丁错误.
正确的有两个,故选B.
B
【解析】根据同角的余角相等可得,∠AOB=∠COD,而不会得出∠AOB+∠COD=90°,故甲正确,丙错误;∠BOC+∠AOD=∠BOC+∠AOB+∠BOD=∠AOC+∠BOD=90°+90°=180°,故乙正确;
图中小于平角的角有∠COD,∠BOD,∠AOD,∠BOC,∠AOC,∠AOB六个,故丁错误.
正确的有两个,故选B. 如图,数轴上有A、B、C、D四个整数点(即各点均表示整数),且3AB=BC=2CD.若A、D两点所表示的数分别是﹣6和5,则线段AC的中点所表示的数是( )

A. ﹣3 B. ﹣1 C. 3 D. ﹣2
 D
【解析】首先设BC为6x,根据3AB=BC=2CD表示出AB=2x,CD=3x,然后根据线段AD的长度建立方程,进而求出点C所表示的数,再利用两点之间的中点公式即可得出答案.
【解析】
设BC=6x,
∵3AB=BC=2CD,
∴AB=2x,CD=3x,
∴AD=AB+BC+CD=11x,
∵A,D两点所表示的数分别是?6和5,
∴AD=11,
...
D
【解析】首先设BC为6x,根据3AB=BC=2CD表示出AB=2x,CD=3x,然后根据线段AD的长度建立方程,进而求出点C所表示的数,再利用两点之间的中点公式即可得出答案.
【解析】
设BC=6x,
∵3AB=BC=2CD,
∴AB=2x,CD=3x,
∴AD=AB+BC+CD=11x,
∵A,D两点所表示的数分别是?6和5,
∴AD=11,
... 若(2x+a)(x﹣1)的结果中不含x的一次项,则a=_____.
 2.
【解析】试题解析:(2x+a)(x-1)=2x2+(a-2)x-a,
由结果中不含x的一次项,得到a-2=0,即a=2.
2.
【解析】试题解析:(2x+a)(x-1)=2x2+(a-2)x-a,
由结果中不含x的一次项,得到a-2=0,即a=2. 如图所示,某船上午11时30分在A处观测海岛B在北偏东60°方向,该船以每小时10海里的速度航行到C处,再观测海岛B在北偏东30°方向,又以同样的速度继续航行到D处,再观测海岛在北偏西30°方向,当轮船到达C处时恰好与海岛B相距20海里,请你确定轮船到达C处和D处的时间.
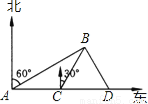
 轮船到达C处的时间为13时30分,到达D处的时间15时30分
【解析】试题分析:首先根据题意得出∠BAC=30°,∠BCD=60°,从而得出∠BAC=∠CBA=30°,则AC=BC,根据题意得出∠BDC=60°,得到△BCD为等边三角形,则BC=AC=CD=BD=20,从而求出船从A点到达C点所用的时间和船从C点到达D点所用的时间.
试题解析:∵在A处观测海岛B在北偏东60°方向,∴∠...
轮船到达C处的时间为13时30分,到达D处的时间15时30分
【解析】试题分析:首先根据题意得出∠BAC=30°,∠BCD=60°,从而得出∠BAC=∠CBA=30°,则AC=BC,根据题意得出∠BDC=60°,得到△BCD为等边三角形,则BC=AC=CD=BD=20,从而求出船从A点到达C点所用的时间和船从C点到达D点所用的时间.
试题解析:∵在A处观测海岛B在北偏东60°方向,∴∠...