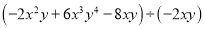题目内容
如果(2x+m)(x-5)展开后的结果中不含x的一次项,那么m等于( )
A. 5 B. -10 C. -5 D. 10
 D
【解析】(2x+m)(x-5)=2x2+mx-10x-5m,因展开后的结果中不含x的一次项,可得m-10=0,解得m=10,故选D.
D
【解析】(2x+m)(x-5)=2x2+mx-10x-5m,因展开后的结果中不含x的一次项,可得m-10=0,解得m=10,故选D.
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
如图所示,D,E分别是△ABC的边AC.BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为 ( )
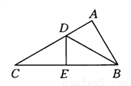
A. 15° B. 20° C. 25° D. 30°
 D
【解析】∵△ADB≌△EDB≌△EDC,
∴∠C=∠DBE=∠DBA,∠DEC=∠DEB=∠A=90°,
∴∠C=30°
故选D.
D
【解析】∵△ADB≌△EDB≌△EDC,
∴∠C=∠DBE=∠DBA,∠DEC=∠DEB=∠A=90°,
∴∠C=30°
故选D. 已知(x-2 015)2+(x-2 017)2=34,则(x-2 016)2的值是( )
A. 4 B. 8 C. 12 D. 16
 D
【解析】(x-2 015)2+(x-2 017)2
=(x-2 016+1)2+(x-2 016-1)2
=
==34
∴
故选D.
D
【解析】(x-2 015)2+(x-2 017)2
=(x-2 016+1)2+(x-2 016-1)2
=
==34
∴
故选D. 多项式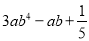 有______项,它们分别是______
有______项,它们分别是______
 3
【解析】多项式中每个单项式叫做多项式的项,由此可得多项式有3项,它们分别是.
3
【解析】多项式中每个单项式叫做多项式的项,由此可得多项式有3项,它们分别是. 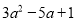 与
与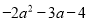 的和为 ( )
的和为 ( )
A. 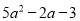 B.
B. 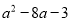 C.
C. 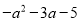 D.
D. 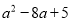
 B
【解析】由题意可得: +=,故选B.
B
【解析】由题意可得: +=,故选B. 数学课上,刘老师和学生做一个猜数游戏,他让学生按照以下步骤进行计算:
①任想一个两位数a,把a乘以2,再加上9,把所得的和再乘以2;
②把a乘以2,再加上30,把所得的和除以2;
③把①所得的结果减去②所得的结果,这个差即为最后的结果.
刘老师说:只要你告诉我最后的结果,我就能猜出你最初想的两位数a是多少.
这时学生小华计算的结果是69,刘老师立即猜出周晓晓最初想的两位数是22.
(1)用含a的代数式表示:步骤①的结果是 步骤②的结果是 步骤③的结果是
(2)若小强按这个猜数游戏的步骤计算后,说出的最后的结果是150,那么小强最初想的两位数是多少?
 (1)4a+18 a+15 3a+3(2)49
【解析】试题分析:(1)根据①②③步骤列出代数式,化简后即可得出结论;
(2)结合(1)可知3a+3=150,解之即可得出结论.
试题解析:
【解析】
(1)由题意可知,第①步运算的结果为:2(2a+9)=4a+18;
第②步运算的结果为: (2a+30)=a+15;
第③步运算的为:(4a+18)-(a+15)...
(1)4a+18 a+15 3a+3(2)49
【解析】试题分析:(1)根据①②③步骤列出代数式,化简后即可得出结论;
(2)结合(1)可知3a+3=150,解之即可得出结论.
试题解析:
【解析】
(1)由题意可知,第①步运算的结果为:2(2a+9)=4a+18;
第②步运算的结果为: (2a+30)=a+15;
第③步运算的为:(4a+18)-(a+15)... 如图,数轴上有A、B、C、D四个整数点(即各点均表示整数),且3AB=BC=2CD.若A、D两点所表示的数分别是﹣6和5,则线段AC的中点所表示的数是( )

A. ﹣3 B. ﹣1 C. 3 D. ﹣2
 D
【解析】首先设BC为6x,根据3AB=BC=2CD表示出AB=2x,CD=3x,然后根据线段AD的长度建立方程,进而求出点C所表示的数,再利用两点之间的中点公式即可得出答案.
【解析】
设BC=6x,
∵3AB=BC=2CD,
∴AB=2x,CD=3x,
∴AD=AB+BC+CD=11x,
∵A,D两点所表示的数分别是?6和5,
∴AD=11,
...
D
【解析】首先设BC为6x,根据3AB=BC=2CD表示出AB=2x,CD=3x,然后根据线段AD的长度建立方程,进而求出点C所表示的数,再利用两点之间的中点公式即可得出答案.
【解析】
设BC=6x,
∵3AB=BC=2CD,
∴AB=2x,CD=3x,
∴AD=AB+BC+CD=11x,
∵A,D两点所表示的数分别是?6和5,
∴AD=11,
... 在一个口袋中,共有50个球,其中白球20个,红球20个,其余为篮球,从中任摸一球,摸到不是白球的概率是( )
A. 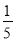 B.
B. 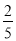 C.
C. 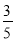 D.
D. 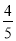
 C
【解析】口袋中,共有50个球,其中白球20个,那么不是白球的球共有30个,所以摸到不是白球的概率是,故选C.
C
【解析】口袋中,共有50个球,其中白球20个,那么不是白球的球共有30个,所以摸到不是白球的概率是,故选C.