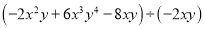题目内容
下面是两个可以自由转动的转盘,转动转盘,分别计算转盘停止后,指针落在红色区域的概率.
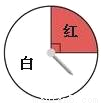
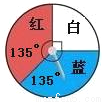
 【解析】分析:本题考察对概率意义的理解,关键是根据图示,由圆心角的度数求出概率.
本题解析:
由图可以看出,在第一个转盘内,红色区域的圆心角是90°,因此可以算得指针落在红色区域的概率是;在第二个转盘内,红色区域的圆心角是135°,因此可以算得指针落在红色区域的概率是 .
【解析】分析:本题考察对概率意义的理解,关键是根据图示,由圆心角的度数求出概率.
本题解析:
由图可以看出,在第一个转盘内,红色区域的圆心角是90°,因此可以算得指针落在红色区域的概率是;在第二个转盘内,红色区域的圆心角是135°,因此可以算得指针落在红色区域的概率是 .
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
如图,数轴上有A、B、C、D四个整数点(即各点均表示整数),且3AB=BC=2CD.若A、D两点所表示的数分别是﹣6和5,则线段AC的中点所表示的数是( )

A. ﹣3 B. ﹣1 C. 3 D. ﹣2
 D
【解析】首先设BC为6x,根据3AB=BC=2CD表示出AB=2x,CD=3x,然后根据线段AD的长度建立方程,进而求出点C所表示的数,再利用两点之间的中点公式即可得出答案.
【解析】
设BC=6x,
∵3AB=BC=2CD,
∴AB=2x,CD=3x,
∴AD=AB+BC+CD=11x,
∵A,D两点所表示的数分别是?6和5,
∴AD=11,
...
D
【解析】首先设BC为6x,根据3AB=BC=2CD表示出AB=2x,CD=3x,然后根据线段AD的长度建立方程,进而求出点C所表示的数,再利用两点之间的中点公式即可得出答案.
【解析】
设BC=6x,
∵3AB=BC=2CD,
∴AB=2x,CD=3x,
∴AD=AB+BC+CD=11x,
∵A,D两点所表示的数分别是?6和5,
∴AD=11,
... 若(2x+a)(x﹣1)的结果中不含x的一次项,则a=_____.
 2.
【解析】试题解析:(2x+a)(x-1)=2x2+(a-2)x-a,
由结果中不含x的一次项,得到a-2=0,即a=2.
2.
【解析】试题解析:(2x+a)(x-1)=2x2+(a-2)x-a,
由结果中不含x的一次项,得到a-2=0,即a=2. 下列多项式的乘法中,可以用平方差公式计算的是( ).
A.  B.
B.  C.
C.  D.
D. 
 C
【解析】试题解析:A.(a+b)(b+a),不符合平方差公式;
B.(?a+b)(a?b)两项都互为相反数,不符合平方差公式;
C. 二项式中有一项完全相同,另一项互为相反数,符合平方差公式;
D. 两项都不相同,不符合平方差公式.
故选C.
C
【解析】试题解析:A.(a+b)(b+a),不符合平方差公式;
B.(?a+b)(a?b)两项都互为相反数,不符合平方差公式;
C. 二项式中有一项完全相同,另一项互为相反数,符合平方差公式;
D. 两项都不相同,不符合平方差公式.
故选C. 一副扑克牌去掉大王、小王后随意抽取一张,抽到方块的概率是______,抽到3的概率是______.
 【解析】一副扑克牌去掉大王、小王后还有52张,其中方块有13张,所以随意抽取一张,抽到方块的概率是;在这52张中,3共有4张,因此抽到3的概率是.故答案为: .
【解析】一副扑克牌去掉大王、小王后还有52张,其中方块有13张,所以随意抽取一张,抽到方块的概率是;在这52张中,3共有4张,因此抽到3的概率是.故答案为: . 在一个口袋中,共有50个球,其中白球20个,红球20个,其余为篮球,从中任摸一球,摸到不是白球的概率是( )
A. 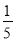 B.
B. 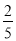 C.
C. 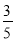 D.
D. 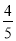
 C
【解析】口袋中,共有50个球,其中白球20个,那么不是白球的球共有30个,所以摸到不是白球的概率是,故选C.
C
【解析】口袋中,共有50个球,其中白球20个,那么不是白球的球共有30个,所以摸到不是白球的概率是,故选C. 如图所示,某船上午11时30分在A处观测海岛B在北偏东60°方向,该船以每小时10海里的速度航行到C处,再观测海岛B在北偏东30°方向,又以同样的速度继续航行到D处,再观测海岛在北偏西30°方向,当轮船到达C处时恰好与海岛B相距20海里,请你确定轮船到达C处和D处的时间.
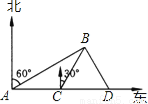
 轮船到达C处的时间为13时30分,到达D处的时间15时30分
【解析】试题分析:首先根据题意得出∠BAC=30°,∠BCD=60°,从而得出∠BAC=∠CBA=30°,则AC=BC,根据题意得出∠BDC=60°,得到△BCD为等边三角形,则BC=AC=CD=BD=20,从而求出船从A点到达C点所用的时间和船从C点到达D点所用的时间.
试题解析:∵在A处观测海岛B在北偏东60°方向,∴∠...
轮船到达C处的时间为13时30分,到达D处的时间15时30分
【解析】试题分析:首先根据题意得出∠BAC=30°,∠BCD=60°,从而得出∠BAC=∠CBA=30°,则AC=BC,根据题意得出∠BDC=60°,得到△BCD为等边三角形,则BC=AC=CD=BD=20,从而求出船从A点到达C点所用的时间和船从C点到达D点所用的时间.
试题解析:∵在A处观测海岛B在北偏东60°方向,∴∠... 下面四个图形中,线段BE是△ABC的高的图是( )
A. 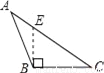 B.
B. 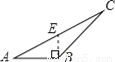 C.
C. 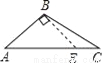 D.
D. 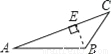
 D
【解析】试题分析:根据三角形高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高,再结合图形进行判断.
【解析】
线段BE是△ABC的高的图是选项D.
故选D.
D
【解析】试题分析:根据三角形高的画法知,过点B作AC边上的高,垂足为E,其中线段BE是△ABC的高,再结合图形进行判断.
【解析】
线段BE是△ABC的高的图是选项D.
故选D.