题目内容
20.计算:(1)$\sqrt{48}÷\sqrt{3}-\sqrt{\frac{1}{2}}×\sqrt{12}+\sqrt{24}$
(2)$\frac{1}{x}+\frac{{{x^2}-4}}{{2{x^2}+4x}}÷({1-\frac{x}{x-2}})$.
分析 (1)首先进行二次根式的乘除法运算,然后进行二次根式的化简及同类二次根式的合并.
(2)首先进行分式的化简,然后进行分式的除法运算及合并.
解答 解:(1)原式=4$\sqrt{3}$$÷\sqrt{3}$-$\frac{\sqrt{2}}{2}$×2$\sqrt{3}$+2$\sqrt{6}$
=4-$\sqrt{6}$+2$\sqrt{6}$
=$4+\sqrt{6}$;
(2)原式=$\frac{1}{x}$+$\frac{(x-2)(x+2)}{2x(x+2)}$÷$\frac{x-2-x}{x-2}$
=$\frac{1}{x}$+$\frac{x-2}{2x}$÷(-$\frac{2}{x-2}$)
=$\frac{1}{x}$-$\frac{{(x-2)}^{2}}{4x}$
=$\frac{{4-x}^{2}-4+4x}{4x}$
=$\frac{{4x-x}^{2}}{4x}$
=$\frac{4-x}{4}$.
点评 本题考查了二次根式的混合运算及分式的混合运算,解答本题的关键是掌握二次根式的化简及分式的化简.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
11.某市对居民生活用电实行“阶梯电价”收费,具体收费标准见表:
(1)根据题意,填写表格.
(2)设该市一户居民某月用电x千瓦时,当月的电费为y元,写出y与x之间的函数关系式.
当0≤x≤150时,y=0.6x;
当150<x≤300时,y=0.65x-7.5;
当x>300时,y=0.9x-82.5.
(3)一户居民某月的电费为174.5元,求该户居民这个月的用电量.
| 一户居民一个月用电量的范围 | 电费价格(单位:元/千瓦时) |
| 不超过150千瓦时的部分 | 0.6 |
| 超过150千瓦时,但不超过300千瓦时的部分 | 0.65 |
| 超过300千瓦时的部分 | 0.9 |
| 某居民一个月用电量(千瓦时) | 100 | 150 | 200 | 300 | 350 | 400 | … |
| 电费价格(元) | 60 | 90 | 122.5 | 187.5 | 232.5 | 277.5 | … |
当0≤x≤150时,y=0.6x;
当150<x≤300时,y=0.65x-7.5;
当x>300时,y=0.9x-82.5.
(3)一户居民某月的电费为174.5元,求该户居民这个月的用电量.
8.下列从左到右的变形中,是分解因式的是( )
| A. | a2-4a+5=a(a-4)+5 | B. | (x+2)(x+3)=x2+5x+6 | C. | a2-9b2=(a+3b)(a-3b) | D. | x+1=x(1+$\frac{1}{x}$) |
15.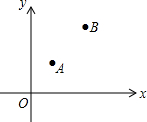 如图,在平面直角坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为( )
如图,在平面直角坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为( )
 如图,在平面直角坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为( )
如图,在平面直角坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使得△PAB的周长最小,则点P的坐标为( )| A. | (0,1) | B. | (0,2) | C. | ($\frac{4}{3}$,0) | D. | (2,0) |
5.[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”[1,m-$\sqrt{2}$]的一次函数是正比例函数,则关于x的方程x+$\frac{1}{m}$=$\sqrt{2}$的解为( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
9.如果三角形的两边长分别为5和7,第三边长为偶数,那么这个三角形的周长可以是( )
| A. | 10 | B. | 11 | C. | 16 | D. | 26 |
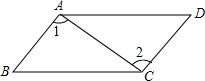 如图,在四边形ABCD中,∠BAD=∠BCD,∠1=∠2,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠BAD=∠BCD,∠1=∠2,求证:四边形ABCD是平行四边形.