题目内容

9．如果三角形的两边长分别为5和7，第三边长为偶数，那么这个三角形的周长可以是（　　）
A．10B．11C．16D．26

分析 利用三角形三边关系定理，先确定第三边的范围，进而就可以求出第三边的长，从而求得三角形的周长．

解答 解：设第三边为acm，根据三角形的三边关系知，2＜a＜12．
由于第三边的长为偶数，
则a可以为4cm或6cm或8cm或10cm．
∴三角形的周长是 5+7+4=16cm或5+7+6=18cm或5+7+8=20cm或5+7+10=22cm．
故选C．

点评 考查了三角形三边关系，要注意三角形形成的条件：任意两边之和大于第三边，任意两边之差小于第三边，当题目指代不明时，一定要分情况讨论，把符合条件的保留下来，不符合的舍去．

练习册系列答案
相关题目
19．已知a、b满足方程组$\left\{\begin{array}{l}{4a-3b=22}\\{2a+b=16}\end{array}\right.$
（1）求a，b的值；
（2）若a、b是一个等腰三角形的两边长，求这个等腰三角形的周长．
20．计算：
（1）$\sqrt{48}÷\sqrt{3}-\sqrt{\frac{1}{2}}×\sqrt{12}+\sqrt{24}$
（2）$\frac{1}{x}+\frac{{{x^2}-4}}{{2{x^2}+4x}}÷（{1-\frac{x}{x-2}}）$．
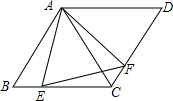17．如图，在菱形ABCD中，AB=4，∠BAD=120°，△AEF为等边三角形，点E，F分别在菱形的边BC，CD上滑动，且E，F不与B，C，D重合．
（1）求证：BE=CF；
（2）当点E，F在BC，CD上滑动时，四边形AECF的面积是否发生变化？如果不变，求出这个定值，如果变化，说明理由．
4．如图，△ABC是以BC为底边的等腰三角形，点A、C分别是一次函数$y=-\frac{3}{4}x+3$的图象与y轴、x轴的交点，点B在二次函数$y=\frac{1}{8}{x^2}+bx+c$的图象上，且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形．
（1）试求b、c的值，并写出该二次函数的解析式；
（2）动点P从A到D，同时动点Q从C到A都以每秒1个单位的速度运动，问：
①当P运动到何处时，△APQ是直角三角形？
②当P运动到何处时，四边形PDCQ的面积最小？此时四边形PDCQ的面积是多少？
14．现有如图①所示的两种瓷砖．请从这两种瓷砖中各选2块，拼成一个新的正方形地板图案，使拼铺的图案成轴对称图形或中心对称图形（如示例图②）．
（要求：分别在图③、图④中各设计一种与示例图不同的拼法，这两种拼法各不相同，且在图③拼成的图案是轴对称图形，在图④拼成的图案既是轴对称图形，又是中心对称图形．）
1．如图，水以恒速（即单位时间内注入水的体积相同）注入如图的容器中，容器中水的高度h与时间t的函数关系图象可能为（　　）
A．B．C．D．
18．下列运算正确的是（　　）
A．2a4•3a5=6a20B．a-4÷a-6=a2C．（a2）3=a5D．（3a2）2=6a4
19．计算：
（1）$\sqrt{2{a}^{3}}$•$\sqrt{8a}$（a≥0）；    
（2）$\sqrt{6}$×（2$\sqrt{3}$-3$\sqrt{\frac{1}{3}}$）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网