题目内容
15．
如图，在平面直角坐标系中，已知A（1，1）、B（3，5），要在y轴上找一点P，使得△PAB的周长最小，则点P的坐标为（ ）| A． | （0，1） | B． | （0，2） | C． | （$\frac{4}{3}$，0） | D． | （2，0） |
分析 作点A关于y轴的对称点A′，连接A′B交y轴于点P，求出P点坐标即可．
解答 解：如图1，作点A关于y轴的对称点A′，连接A′B交y轴于点P，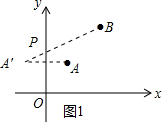
∵A（1，1），
∴A′（-1，1），
设直线A′B的解析式为y=kx+b（k≠0），
∴$\left\{\begin{array}{l}{3k+b=5}\\{-k+b=1}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$，
∴直线A′B的解析式为y=x+2，
当x=0时，y=2，
∴P（0，2）．
故选B．
点评 本题考查的是轴对称-最短路线问题，熟知“两点之间，线段最短”是解答此题的关键．
练习册系列答案
相关题目
6．某校初三（2）班40名同学为“希望工程”捐款，共捐款100元，捐款情况如表：
表格中捐款2元和3元的人数不小心被墨水污染已经看不清楚．
若设捐款2元的有x名同学，捐款3元的有y名同学，根据题意，可得方程组（ ）
| 捐款（元） | 1 | 2 | 3 | 4 |
| 人数（人） | 6 | ● | ● | 7 |
若设捐款2元的有x名同学，捐款3元的有y名同学，根据题意，可得方程组（ ）
| A． | $\left\{\begin{array}{l}{x+y=27}\\{2x+3y=66}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=27}\\{2x+3y=100}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{x+y=27}\\{3x+2y=66}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=27}\\{3x+2y=100}\end{array}\right.$ |
在如图的正方形网格中，有一个格点三角形ABC（即三角形的顶点都在格点上）．
如图，把“QQ”笑脸放在直角坐标系中，已知左眼A的坐标是（-2，3），嘴唇C的坐标为（-1，1），若把此“QQ”笑脸向右平移3个单位长度后，则与右眼B对应的点的坐标是（3，3）．
如图，△ABC是以BC为底边的等腰三角形，点A、C分别是一次函数$y=-\frac{3}{4}x+3$的图象与y轴、x轴的交点，点B在二次函数$y=\frac{1}{8}{x^2}+bx+c$的图象上，且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形．
5．在直角坐标系中，将点P（-3，5）向右平移2个单位长度，再向上平移1个单位长度，可以得到对应点P1的坐标为（ ）
| A． | （-3，3） | B． | （-3，6） | C． | （-1，5） | D． | （-1，6） |