题目内容
17.在Rt△ABC中,AB=BC=5,∠B=90°,将一块等腰直角三角板的直角顶点放在斜边AC的中点O处,将三角板绕点O旋转,三角板的两直角边分别交AB,BC或其延长线于E,F两点,如图①与②是旋转三角板所得图形的两种情况.(1)三角板绕点O旋转,△OFC是否能成为等腰三角形?若能,指出所有情况(即给出△OFC是等腰直角三角形时BF的长),若不能,请说明理由;
(2)三角板绕点O旋转,线段OE和OF之间有什么数量关系?用图①或②加以证明.
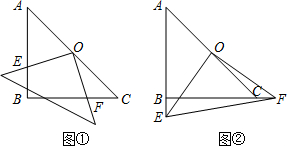
分析 (1)由题意可知,①当F为BC的中点时,由AB=BC=5,可以推出CF和OF的长度,即可推出BF的长度,②当B与F重合时,③当OC=FC时,根据直角三角形的相关性质,即可推出OF的长度,即可推出BF的长度;
(2)连接OB,由已知条件推出△OEB≌△OFC,即可推出OE=OF.
解答 解:(1)△OFC是能成为等腰直角三角形,
①当F为BC的中点时,
∵O点为AC的中点,
∴OF∥AB,
∴CF=OF=$\frac{1}{2}$AB=$\frac{5}{2}$,
∵AB=BC=5,
∴BF=$\frac{5}{2}$,
②当B与F重合时,
∵OF=OC=$\frac{5}{2}$$\sqrt{2}$,
∴BF=0;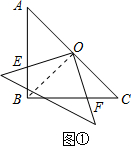
(2)如图①,连接OB,
∵由(1)的结论可知,BO=OC=$\frac{5}{2}$$\sqrt{2}$,
在△OEB与△OFC中,$\left\{\begin{array}{l}{∠OBE=∠C}\\{OB=OC}\\{∠EOB=∠FOC}\end{array}\right.$,
∴△OEB≌△OFC(ASA),
∴OE=OF.
点评 本题主要考查全等三角形的判定和性质、等腰直角三角形的性质、旋转的性质,解题的关键在于作好辅助线,构建全等的三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
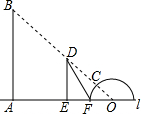 学生在操场上利用三角函数测量旗杆AB的高,直线l为水平地面,两个同学把30°的三角板和量角器按如图所示的方式垂直放在地面上,量角器的零刻度线与地面重合,此时旗杆顶部B的影子恰好落在三角形板的顶点D处和量角器37°的刻度C处,已知三角形板的边DE=60厘米,量角器的半径r=25厘米,量角器的圆心O到A的距离为5米.
学生在操场上利用三角函数测量旗杆AB的高,直线l为水平地面,两个同学把30°的三角板和量角器按如图所示的方式垂直放在地面上,量角器的零刻度线与地面重合,此时旗杆顶部B的影子恰好落在三角形板的顶点D处和量角器37°的刻度C处,已知三角形板的边DE=60厘米,量角器的半径r=25厘米,量角器的圆心O到A的距离为5米. 已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,沿AC方向,以每秒1个单位的速度向终点C运动,设点P运动时间为t秒.
已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,沿AC方向,以每秒1个单位的速度向终点C运动,设点P运动时间为t秒.