题目内容
2. 已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,沿AC方向,以每秒1个单位的速度向终点C运动,设点P运动时间为t秒.
已知数轴上有A、B、C三点,分别表示有理数-26,-10,10,动点P从A出发,沿AC方向,以每秒1个单位的速度向终点C运动,设点P运动时间为t秒.(1)用含t的代数式表示点P到点A、C的距离,PA=t;PC=36-t.
(2)当点P运动到点B时,点Q从C点出发,沿CA方向,以每秒3个单位的速度向A点运动,当其中一点到达目的地时,另一点也停止运动.
①当t=21,点P、Q相遇,此时点Q运动了5秒.
②请用含t的代数式表示出在P、Q同时运动的过程中PQ的长.
分析 (1)根据题意容易得出结果;
(2)①根据路程和=20,列出方程即可求解;
②根据两点间的距离,要对t分类讨论,t不同范围,可得不同PQ.
解答 解:(1)PA=t;PC=36-t;
(2)①有依题意有
t+3(t-16)-16=20,
解得:t=21,
t-16=21-16=5.
故当t=21,点P、Q相遇,此时点Q运动了5秒.
答案为:24或30;
②当16≤t≤21时 PQ=36-t-3(t-16)=84-4t;
当21<t≤28时 PQ=3(t-16)+t-36=4t-84.
故答案为:t,36-t;21,5.
点评 本题考查了数轴,一元一次方程的应用.解答(2)②题,对t分类讨论是解题关键.

练习册系列答案
相关题目
12.某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到设计方案有等腰三角形、正三角形、平行四边形、菱形等四种图案,你认为符合条件的是( )
| A. | 等腰三角形 | B. | 正三角形 | C. | 平行四边形 | D. | 菱形 |
7.二次函数y=2(x-3)2+5的开口方向、对称轴、顶点坐标分别是( )
| A. | 向上、直线x=3、(3,5) | B. | 向上、直线x=3、(-3,5) | ||
| C. | 向下、直线x=3、(3,5) | D. | 向下、直线x=3、(-3,5) |
12.下列方程中是关于x的一元二次方程的是( )
| A. | (x-1)(x+2)=1 | B. | 3x2-2xy-5y2=0 | C. | x2+$\frac{1}{{x}^{2}}$=0 | D. | ax2+bx+c=0 |
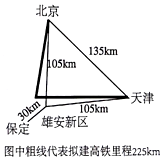 “雄安新区”是中共中央作出“千年大计、国家大事”的重大决策,雄安新区位于北京、天津和保定构成的一个等边三角形腹地,距离北京、天津和保定市分别约105公里、105公里、30公里,如图所示.现拟一列高铁列车从北京经雄安新区到天津比北京与天津的城际特快列车还少用25分,已知高铁速度是城际特快列车的速度2.5倍,高铁列车行驶的里程为225km,北京与天津的里程为135km,求城际特快列车的速度是多少km/h?
“雄安新区”是中共中央作出“千年大计、国家大事”的重大决策,雄安新区位于北京、天津和保定构成的一个等边三角形腹地,距离北京、天津和保定市分别约105公里、105公里、30公里,如图所示.现拟一列高铁列车从北京经雄安新区到天津比北京与天津的城际特快列车还少用25分,已知高铁速度是城际特快列车的速度2.5倍,高铁列车行驶的里程为225km,北京与天津的里程为135km,求城际特快列车的速度是多少km/h?