题目内容
17.将长为10厘米的一条线段用任意方式分成5小段,以这5小段为边可以围成一个五边形,设最长的一段的长度为x厘米,则x的取值范围为2≤x<5.分析 设AB是所围成的五边形ABCDE的某一边(如下图),而线段BC,CD,DE,EA则可看成是点A,B之间的一条折线,因此,AB<BC+CD+DE+EA.如果AB是最长的一段,上面的不等式关系仍然成立,从而可以求出它的取值范围.
解答 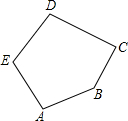 解:设最长的一段AB的长度为x厘米(如上图),则其余4段的和为(10-x)厘米.
解:设最长的一段AB的长度为x厘米(如上图),则其余4段的和为(10-x)厘米.
∵它是最长的边,假定所有边相等,则此时它最小为2,
又由线段基本性质知x<10-x,所以x<5,
∴2≤x<5.
即最长的一段AB的长度必须大于等于2厘米且小于5厘米.
故答案为:2≤x<5.
点评 本题考查了线段的性质,属于基础题,注意两点之间线段最短这一知识点的灵活运用.

练习册系列答案
相关题目
7.已知圆上均匀分布着2000个点,从中均等地选出A、B、C、D四个不同的点,则弦AB与CD相交的概率是( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
5.若不等式组$\left\{\begin{array}{l}{x-b≤0}\\{x+a>0}\end{array}\right.$的解集为2<x≤3,则a,b的值分别为( )
| A. | -2,3 | B. | 2,-3 | C. | 3,-2 | D. | -3,2 |
7.要证明命题“若a>b则a2>b2”是假命题,下列a,b的值能作为反例的是( )
| A. | a=-1,b=2 | B. | a=3,b=2 | C. | a=-1,b=0 | D. | a=-2,b=-1 |
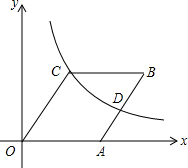 如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.
如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.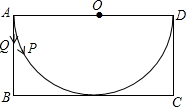 有一张矩形纸片ABCD,其中AD=4cm,其中AD=4cm,上面有一个以AD为直径的半圆,正好与对边BC相切,如图,动点P、Q分别以每秒1cm的速度从A点出发,P点沿$\widehat{AD}$运动到点D,Q点沿A→B→C→D方向运动.(π取3.14)
有一张矩形纸片ABCD,其中AD=4cm,其中AD=4cm,上面有一个以AD为直径的半圆,正好与对边BC相切,如图,动点P、Q分别以每秒1cm的速度从A点出发,P点沿$\widehat{AD}$运动到点D,Q点沿A→B→C→D方向运动.(π取3.14)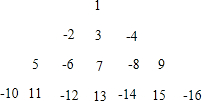 将1,-2,3,-4,5,-6…按一定规律排列如图,则第10行从左到右第9个数是-90.
将1,-2,3,-4,5,-6…按一定规律排列如图,则第10行从左到右第9个数是-90.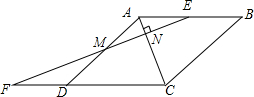 如图,四边形ABCD是菱形,点E为AB的中点,延长CD至F,使得DF=$\frac{1}{2}$CD,连接EF分别交AD,AC于点M,N.
如图,四边形ABCD是菱形,点E为AB的中点,延长CD至F,使得DF=$\frac{1}{2}$CD,连接EF分别交AD,AC于点M,N.