题目内容
5.若不等式组$\left\{\begin{array}{l}{x-b≤0}\\{x+a>0}\end{array}\right.$的解集为2<x≤3,则a,b的值分别为( )| A. | -2,3 | B. | 2,-3 | C. | 3,-2 | D. | -3,2 |
分析 首先解每个不等式,然后根据不等式组的解集即可确定a和b的值.
解答 解:$\left\{\begin{array}{l}{x-b≤0…①}\\{x+a>0…②}\end{array}\right.$,
解①得x≤b,
解②得x>-a.
∵不等式组的解集是2<x≤3.
则-a=2,且b=3.
即a=-2,b=3.
故选A.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.
如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.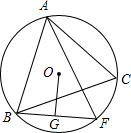 已知△ABC内接于⊙O,F是弧$\widehat{BC}$上一点,OG⊥BF于点G,且OG=$\frac{1}{2}$AC.证明:AF⊥BC.
已知△ABC内接于⊙O,F是弧$\widehat{BC}$上一点,OG⊥BF于点G,且OG=$\frac{1}{2}$AC.证明:AF⊥BC.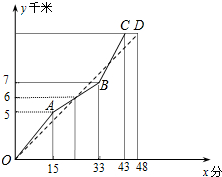 如图,在一次自行车越野赛中,甲、乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线(OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是24<x<38.
如图,在一次自行车越野赛中,甲、乙两名选手所走的路程y(千米)随时间x(分钟)变化的图象(全程)分别用实线(O→A→B→C)与虚线(OD)表示,那么,在本次比赛过程中,乙领先甲时的x的取值范围是24<x<38.