题目内容
8.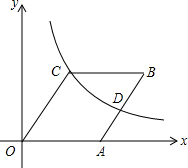 如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.
如图,在菱形OABC中点A在x轴的正半轴上,点B坐标为(8,4)双曲线y=$\frac{k}{x}$(k>0)经过点C,交AB于点D.(1)求双曲线解析式;
(2)求点D坐标.
分析 (1)过点B作BD⊥x轴于点D,设菱形的边长为a,则AD=8-a,BD=4,根据勾股定理求出x的值,进而可得出C点坐标,代入反比例函数的解析式即可;
(2)求出直线AB的解析式与反比例函数的解析式列出方程组,解方程组即可求得交点D的坐标.
解答 解:(1)如图,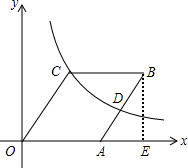
点B作BE⊥x轴于点E,设菱形的边长为x,
∵B(8,4),
∴AE=8-a,BE=4,
在Rt△ABD中,AB2=AE2+BE2,即x2=(8-x)2+42,解得x=5,
∴C(3,4),
∴k=3×4=12,反比例函数解析式为y=$\frac{12}{x}$.
(2)∵点A(5,0),B(8,4),设直线AB为y=kx+b,则$\left\{\begin{array}{l}{5k+b=0}\\{8k+b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-\frac{20}{3}}\end{array}\right.$,
∴直线AB为:y=$\frac{4}{3}$x-$\frac{20}{3}$,
由$\left\{\begin{array}{l}{y=\frac{12}{x}}\\{y=\frac{4}{3}x-\frac{20}{3}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{5+\sqrt{61}}{2}}\\{y=\frac{2}{3}(\sqrt{61}-5)}\end{array}\right.$或$\left\{\begin{array}{l}{x=\frac{5-\sqrt{61}}{2}}\\{y=-\frac{2}{3}(\sqrt{61}+5)}\end{array}\right.$,
∴点D坐标为($\frac{5+\sqrt{61}}{2}$,$\frac{2}{3}$($\sqrt{61}-5$).
点评 本题考查的是菱形的性质,反比例函数图象上点的坐标特点,熟知菱形的性质,反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键,学会用解方程组的思想求还是交点坐标的方法,属于中考常考题型.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案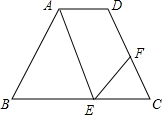 如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°
如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50° 如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.
如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OH⊥MN.