题目内容
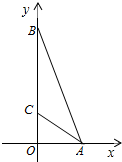如图，在直角坐标系中，AC是Rt△OAB的角平分线，已知点C的坐标是（0，3），AB的长度为12，则△ABC的面积为（ ）| A、15 | B、18 | C、36 | D、60 |
考点：轴对称的性质
专题：
分析：过点C作CD⊥AB于点D，由角平分线的性质可得出CD的长，再根据三角形的面积公式即可得出结论．
解答：
解：过点C作CD⊥AB于点D，
∵C（0，3）
∴OC=3，
∵AC是Rt△OAB的角平分线，OC⊥OA，DC⊥AB，
∴CD=CO=3，
∴S△ABD=
AB•DC=
×12×3=18．
故选B．
解：过点C作CD⊥AB于点D，∵C（0，3）
∴OC=3，
∵AC是Rt△OAB的角平分线，OC⊥OA，DC⊥AB，
∴CD=CO=3，
∴S△ABD=
| 1 |
| 2 |
| 1 |
| 2 |
故选B．
点评：本题考查的是角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解答此题的关键．
练习册系列答案
相关题目
如图，正方形ABCD中，
两块非等腰的三角板（△ABC和△DEC），摆在同一个平面内，其中∠ACB和∠ECD是直角，且∠CAB和∠CDE为30度，点F，G，H分别为边BD、AB、AE上的m等分点，即BF：BD=BG：AB=EH：AE=1：m，连结FG、HG，则FG：HG=（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
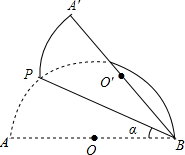如图，AB是半圆O的直径，点P（不与点A，B重合）为半圆上一点．将图形沿BP折叠，分别得到点A，O的对称点A′，O′．设∠ABP=α．
用形状、大小完全相等的下列图形不能进行密铺的是（ ）
| A、等腰三角形 | B、平行四边形 |
| C、正五边形 | D、正六边形 |
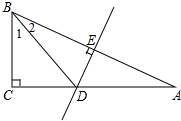如图所示，在△ABC中，∠C=90°，AB的垂直平分线交AC于D点，垂足为E，且∠1=2∠2，求∠A的度数．