题目内容
一次测验中的填空题如下:
(1)当m取1时,一次函数y=(m-2)x+3的图象,y随x的增大而 增大 ;
(2)等腰梯形ABCD,上底AD=2,下底BC=8,∠B=60°,则腰长AB= 6 ;
(3)菱形的边长为6cm,一组相邻角的比为1:2,则菱形的两条对角线的长分别为 6cm和6
cm ;
(4)如果一个多边形的内角和为900°,则这个多边形是 五 边形;
你认为正确的添空个数是( )
(1)当m取1时,一次函数y=(m-2)x+3的图象,y随x的增大而 增大 ;
(2)等腰梯形ABCD,上底AD=2,下底BC=8,∠B=60°,则腰长AB= 6 ;
(3)菱形的边长为6cm,一组相邻角的比为1:2,则菱形的两条对角线的长分别为 6cm和6
| 3 |
(4)如果一个多边形的内角和为900°,则这个多边形是 五 边形;
你认为正确的添空个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:等腰梯形的性质,一次函数图象与系数的关系,多边形内角与外角,菱形的性质
专题:
分析:(1)当k<0,一次函数为减函数,即可得出;
(2)根据等腰梯形的性质,如图,构建直角三角形,即可得出;
(3)根据菱形的性质,结合直角三角形,解答出即可;
(4)根据多边形的内角和计算公式和多边形的外角和是360°,找出等量关系,即可解答出.
(2)根据等腰梯形的性质,如图,构建直角三角形,即可得出;
(3)根据菱形的性质,结合直角三角形,解答出即可;
(4)根据多边形的内角和计算公式和多边形的外角和是360°,找出等量关系,即可解答出.
解答:解:(1)当m=1,一次函数y=-x+3是减函数,y随x的增大而减小;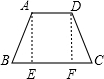
故本项错误;
(2)如图,作AE⊥BC,DF⊥BC,
∴在等腰梯形ABCD中,BE=FC=3,
又∵∠B=60°,
∴AB=2BE=6;
故本项正确;
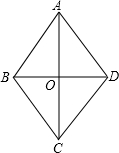
(3)如图,由题意可得,
在菱形ABCD中,∠BAD=60°,∠ABC=120°,
∴∠ABO=60°,∠BAO=30°,
∴OB=
AB=3cm,OA=3
cm,
∴BD=6cm,AC=6
cm;
故本项正确;
(4)由(n-2)×180°+180°=360°×3,
解得,n=7;
故本项错误.
故选B.

故本项错误;
(2)如图,作AE⊥BC,DF⊥BC,
∴在等腰梯形ABCD中,BE=FC=3,
又∵∠B=60°,
∴AB=2BE=6;
故本项正确;

(3)如图,由题意可得,
在菱形ABCD中,∠BAD=60°,∠ABC=120°,
∴∠ABO=60°,∠BAO=30°,
∴OB=
| 1 |
| 2 |
| 3 |
∴BD=6cm,AC=6
| 3 |
故本项正确;
(4)由(n-2)×180°+180°=360°×3,
解得,n=7;
故本项错误.
故选B.
点评:本题主要考查了一次函数、多边形内角和及等腰梯形、菱形的性质,本题涉及的知识点较多,考查了学生对于知识的综合运用能力.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
根据下列已知条件,能画出唯一△ABC的是( )
| A、AB=3,BC=4,AC=7 |
| B、AB=4,BC=3,∠C=30° |
| C、∠A=30°,AB=3,∠B=45° |
| D、∠C=90°,AB=4 |
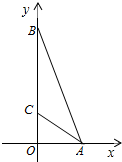 如图,在直角坐标系中,AC是Rt△OAB的角平分线,已知点C的坐标是(0,3),AB的长度为12,则△ABC的面积为( )
如图,在直角坐标系中,AC是Rt△OAB的角平分线,已知点C的坐标是(0,3),AB的长度为12,则△ABC的面积为( )| A、15 | B、18 | C、36 | D、60 |
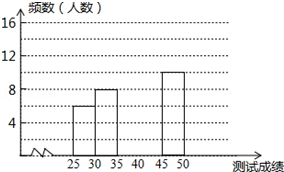 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表: 如图,在Rt△ABC中,∠C=90°,BC=3,AC=3
如图,在Rt△ABC中,∠C=90°,BC=3,AC=3