题目内容
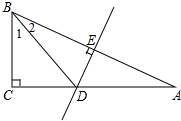如图所示，在△ABC中，∠C=90°，AB的垂直平分线交AC于D点，垂足为E，且∠1=2∠2，求∠A的度数．考点：线段垂直平分线的性质
专题：
分析：证明∠2=∠A（设为α），∠1+∠BDC=90°，得到4α=90°，即可解决问题．
解答：解：∵AB的垂直平分线交AC于D点，
∴DB=DA，∠2=∠A（设为α），
∴∠BDC=∠2+∠A=2α；
∵∠C=90°，∠1=2∠2，
∴∠1+∠BDC=90°，即4α=90°，
∴α=22.5°，
即∠A=22.5°．
∴DB=DA，∠2=∠A（设为α），
∴∠BDC=∠2+∠A=2α；
∵∠C=90°，∠1=2∠2，
∴∠1+∠BDC=90°，即4α=90°，
∴α=22.5°，
即∠A=22.5°．
点评：该题主要考查了线段垂直平分线的性质、直角三角形的性质、三角形的外角性质及其应用问题；对综合运用能力提出了一定的要求．
练习册系列答案
相关题目
根据下列已知条件，能画出唯一△ABC的是（ ）
| A、AB=3，BC=4，AC=7 |
| B、AB=4，BC=3，∠C=30° |
| C、∠A=30°，AB=3，∠B=45° |
| D、∠C=90°，AB=4 |
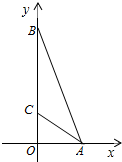如图，在直角坐标系中，AC是Rt△OAB的角平分线，已知点C的坐标是（0，3），AB的长度为12，则△ABC的面积为（ ）| A、15 | B、18 | C、36 | D、60 |
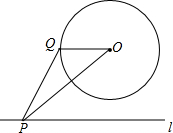如图，⊙O的半径为1，点O到直线l的距离为3，点P是直线l上的一个动点，PQ切⊙O于点Q，则PQ的最小值为
下列各式成立的是（ ）
A、9=
| ||
B、
| ||
C、
| ||
D、
|