题目内容
 两块非等腰的三角板(△ABC和△DEC),摆在同一个平面内,其中∠ACB和∠ECD是直角,且∠CAB和∠CDE为30度,点F,G,H分别为边BD、AB、AE上的m等分点,即BF:BD=BG:AB=EH:AE=1:m,连结FG、HG,则FG:HG=( )
两块非等腰的三角板(△ABC和△DEC),摆在同一个平面内,其中∠ACB和∠ECD是直角,且∠CAB和∠CDE为30度,点F,G,H分别为边BD、AB、AE上的m等分点,即BF:BD=BG:AB=EH:AE=1:m,连结FG、HG,则FG:HG=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:相似三角形的判定与性质
专题:
分析:如图,作辅助线;证明△BFG∽△BDA,得到FG=
;证明GH=
BE;进而得到
=
•
;证明△BCE∽△ACD,得到
=
=
,即可解决问题.
| AD |
| m |
| m-1 |
| m |
| FG |
| GH |
| 1 |
| m-1 |
| AD |
| BE |
| AD |
| BE |
| AC |
| BC |
| 3 |
解答: 解:如图,连接BE、AD;
解:如图,连接BE、AD;
∵BF:BD=BG:AB=EH:AE,
∴GF∥AD、GH∥BE;
∴△BFG∽△BDA,
∴
=
=
,
∴FG=
①;同理可求:
GH=
BE②;
由
得:
=
•
;
∵∠ACB=∠DCE=90°,且∠CAB=∠CDE=30°,
∴∠BCE=∠ACD,
=
=
,
∴△BCE∽△ACD,
∴
=
=
,
∴
=
,
故选C.
 解:如图,连接BE、AD;
解:如图,连接BE、AD;∵BF:BD=BG:AB=EH:AE,
∴GF∥AD、GH∥BE;
∴△BFG∽△BDA,
∴
| FG |
| AD |
| BF |
| BD |
| 1 |
| m |
∴FG=
| AD |
| m |
GH=
| m-1 |
| m |
由
| ① |
| ② |
| FG |
| GH |
| 1 |
| m-1 |
| AD |
| BE |
∵∠ACB=∠DCE=90°,且∠CAB=∠CDE=30°,
∴∠BCE=∠ACD,
| BC |
| AC |
| CE |
| DC |
| 1 | ||
|
∴△BCE∽△ACD,
∴
| AD |
| BE |
| AC |
| BC |
| 3 |
∴
| FG |
| GH |
| ||
| m-1 |
故选C.
点评:该题主要考查了相似三角形的判定及其性质定理的应用问题;同时还渗透了对平行线性质定理的考查.

练习册系列答案
相关题目
计算-t-2t-3t=( )
| A、-4t |
| B、-5t |
| C、-6t |
| D、-6t3 |
根据下列已知条件,能画出唯一△ABC的是( )
| A、AB=3,BC=4,AC=7 |
| B、AB=4,BC=3,∠C=30° |
| C、∠A=30°,AB=3,∠B=45° |
| D、∠C=90°,AB=4 |
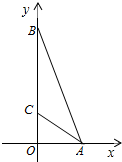 如图,在直角坐标系中,AC是Rt△OAB的角平分线,已知点C的坐标是(0,3),AB的长度为12,则△ABC的面积为( )
如图,在直角坐标系中,AC是Rt△OAB的角平分线,已知点C的坐标是(0,3),AB的长度为12,则△ABC的面积为( )| A、15 | B、18 | C、36 | D、60 |
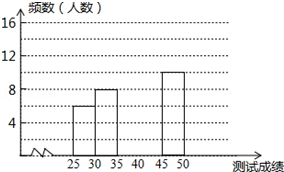 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表: