题目内容
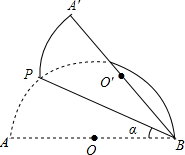 如图,AB是半圆O的直径,点P(不与点A,B重合)为半圆上一点.将图形沿BP折叠,分别得到点A,O的对称点A′,O′.设∠ABP=α.
如图,AB是半圆O的直径,点P(不与点A,B重合)为半圆上一点.将图形沿BP折叠,分别得到点A,O的对称点A′,O′.设∠ABP=α.(1)当α=10°时,∠ABA′
(2)当点O′落在
 |
| PB |
考点:翻折变换(折叠问题),等边三角形的判定与性质
专题:
分析:(1)由∠ABP=∠A′BP=10°,即可解决问题.
(2)如图,作辅助线;证明△OBO′为等边三角形,即可解决问题.
(2)如图,作辅助线;证明△OBO′为等边三角形,即可解决问题.
解答: 解:(1)由翻折变换的性质得:
解:(1)由翻折变换的性质得:
∠ABP=∠A′BP=10°,
∴∠ABA′=20°.
故答案为20.
(2)如图,连接OO′;
∵点O′落在
上,
∴OO′=OB;
∵PB⊥OO′,且平分OO′,
∴BO′=BO,
∴△OBO′为等边三角形,
∴∠ABA′=60°,
∴α=30°.
 解:(1)由翻折变换的性质得:
解:(1)由翻折变换的性质得:∠ABP=∠A′BP=10°,
∴∠ABA′=20°.
故答案为20.
(2)如图,连接OO′;
∵点O′落在
 |
| PB |
∴OO′=OB;
∵PB⊥OO′,且平分OO′,
∴BO′=BO,
∴△OBO′为等边三角形,
∴∠ABA′=60°,
∴α=30°.
点评:该题考查了翻折变换的性质及其应用问题;同时还渗透了对圆的性质、等边三角形的判定及其应用的考查;作辅助线是解题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
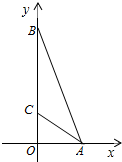 如图,在直角坐标系中,AC是Rt△OAB的角平分线,已知点C的坐标是(0,3),AB的长度为12,则△ABC的面积为( )
如图,在直角坐标系中,AC是Rt△OAB的角平分线,已知点C的坐标是(0,3),AB的长度为12,则△ABC的面积为( )| A、15 | B、18 | C、36 | D、60 |
一元二次方程x2+2x=0的根是( )
| A、x=0 |
| B、x=-2 |
| C、x=0或x=-2 |
| D、x=0或x=2 |
 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表: 如图,在四边形ABCD中,∠B=∠D=90°,∠BAD=60°,CD=11,BC=2,求对角线AC的长.
如图,在四边形ABCD中,∠B=∠D=90°,∠BAD=60°,CD=11,BC=2,求对角线AC的长. 如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“之”相对的面上的汉字是
如图是正方体的一种平面展开图,它的每个面上都有一个汉字,那么在原正方体的表面上,与汉字“之”相对的面上的汉字是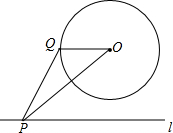 如图,⊙O的半径为1,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为
如图,⊙O的半径为1,点O到直线l的距离为3,点P是直线l上的一个动点,PQ切⊙O于点Q,则PQ的最小值为