题目内容
用形状、大小完全相等的下列图形不能进行密铺的是（ ）
| A、等腰三角形 | B、平行四边形 |
| C、正五边形 | D、正六边形 |
考点：平面镶嵌（密铺）
专题：
分析：分别求出等腰三角形、平行四边形的内角和，各个正多边形的每个内角的度数，结合镶嵌的条件即可作出判断．
解答：解：A、由镶嵌的条件知，在一个顶点处各个内角和为360°．三角形内角和为180°，用6个同一种三角形就可以在同一顶点镶嵌，即能密铺，故此选项不符合题意；
B、由镶嵌的条件知，在一个顶点处各个内角和为360°．平行四边形内角和为360°，用4个同一种平行四边形就可以在同一顶点镶嵌，即能密铺，故此选项不符合题意；
C、正五边形每个内角是：180°-360°÷5=108°，不能整除360°，不能密铺，故符合题意；
D、正六边形每个内角为120°，能整除360°，能密铺，故此选项不符合题意．
故选：C．
B、由镶嵌的条件知，在一个顶点处各个内角和为360°．平行四边形内角和为360°，用4个同一种平行四边形就可以在同一顶点镶嵌，即能密铺，故此选项不符合题意；
C、正五边形每个内角是：180°-360°÷5=108°，不能整除360°，不能密铺，故符合题意；
D、正六边形每个内角为120°，能整除360°，能密铺，故此选项不符合题意．
故选：C．
点评：本题考查了平面镶嵌（密铺），一种正多边形的镶嵌应符合一个内角度数能整除360°，任意多边形能进行镶嵌，说明它的内角和应能整除360°．
练习册系列答案
阅读快车系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，BC=3，AC=3
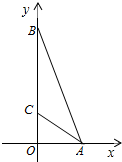如图，在直角坐标系中，AC是Rt△OAB的角平分线，已知点C的坐标是（0，3），AB的长度为12，则△ABC的面积为（ ）| A、15 | B、18 | C、36 | D、60 |