题目内容
 如图,正方形ABCD中,
如图,正方形ABCD中,(1)E为边BC的中点,AE的垂直平分线分别交AB、AE、CD于G、F、H,求
| GF |
| FH |
(2)E的位置改动为边BC上一点,且
| BE |
| EC |
| GF |
| FH |
考点:相似三角形的判定与性质,正方形的性质
专题:
分析:(1)如图1,作辅助线;证明
=
;证明BE=CE,AE=EK,FK=3AF;证明△AGF∽△KHF,得到
=
=
.
(2)如图2,作辅助线;类比(1)中的解法、思路,即可完成(2)的解答.
| AE |
| EK |
| BE |
| CE |
| GF |
| FH |
| AF |
| FK |
| 1 |
| 3 |
(2)如图2,作辅助线;类比(1)中的解法、思路,即可完成(2)的解答.
解答: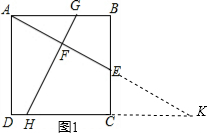 解:(1)如图1,分别延长AE、DC交于点K;
解:(1)如图1,分别延长AE、DC交于点K;
∵四边形ABCD为正方形,
∴AB∥CK,△ABE∽△KCE,
∴
=
;
∵E为边BC的中点,
∴BE=CE,AE=EK;
∵GH平分AE,
∴EK=AE=2AF,FK=3AF;
∵AG∥HK,
∴△AGF∽△KHF,
∴
=
=
.
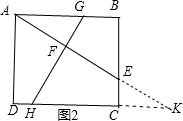 (2)如图2,分别延长AE、DC交于点K;
(2)如图2,分别延长AE、DC交于点K;
∵四边形ABCD为正方形,
∴AB∥CK,△ABE∽△KCE,
∴
=
;
∵
=k,
∴AE=kEK;
∵GH平分AE,
∴AF=EF=
AE=
kEK,FK=
EK;
∵AG∥HK,
∴△AGF∽△KHF,
∴
=
=
.
 解:(1)如图1,分别延长AE、DC交于点K;
解:(1)如图1,分别延长AE、DC交于点K;∵四边形ABCD为正方形,
∴AB∥CK,△ABE∽△KCE,
∴
| AE |
| EK |
| BE |
| CE |
∵E为边BC的中点,
∴BE=CE,AE=EK;
∵GH平分AE,
∴EK=AE=2AF,FK=3AF;
∵AG∥HK,
∴△AGF∽△KHF,
∴
| GF |
| FH |
| AF |
| FK |
| 1 |
| 3 |
 (2)如图2,分别延长AE、DC交于点K;
(2)如图2,分别延长AE、DC交于点K;∵四边形ABCD为正方形,
∴AB∥CK,△ABE∽△KCE,
∴
| AE |
| EK |
| BE |
| CE |
∵
| BE |
| EC |
∴AE=kEK;
∵GH平分AE,
∴AF=EF=
| 1 |
| 2 |
| 1 |
| 2 |
| k+2 |
| 2 |
∵AG∥HK,
∴△AGF∽△KHF,
∴
| FG |
| FH |
| AF |
| FK |
| k |
| k+2 |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是作辅助线,构造相似三角形,灵活运用正方形的性质等几何知识点来分析、判断、推理或解答.

练习册系列答案
相关题目
下列各式运算
(1)-(-a-b)=a-b;(2)5x-(2x-1)-x2=5x-2x-1+x2;
(3)3xy-
(xy-y2)=3xy-
xy+y2; (4)(a3+b3)-3(2a3-3b3)=a3+b3-6a3+9b3
其中去括号不正确的有( )
(1)-(-a-b)=a-b;(2)5x-(2x-1)-x2=5x-2x-1+x2;
(3)3xy-
| 1 |
| 2 |
| 1 |
| 2 |
其中去括号不正确的有( )
| A、(1)(2) |
| B、(1)(2)(3) |
| C、(2)(3)(4) |
| D、(1)(2)(3)(4) |
计算-t-2t-3t=( )
| A、-4t |
| B、-5t |
| C、-6t |
| D、-6t3 |
根据下列已知条件,能画出唯一△ABC的是( )
| A、AB=3,BC=4,AC=7 |
| B、AB=4,BC=3,∠C=30° |
| C、∠A=30°,AB=3,∠B=45° |
| D、∠C=90°,AB=4 |
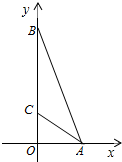 如图,在直角坐标系中,AC是Rt△OAB的角平分线,已知点C的坐标是(0,3),AB的长度为12,则△ABC的面积为( )
如图,在直角坐标系中,AC是Rt△OAB的角平分线,已知点C的坐标是(0,3),AB的长度为12,则△ABC的面积为( )| A、15 | B、18 | C、36 | D、60 |