题目内容
6.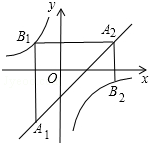 如图,已知点A1,A2,…,An均在直线y=x-2上,点B1,B2,…,Bn均在双曲线y=-$\frac{4}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-2,则a2016=1.
如图,已知点A1,A2,…,An均在直线y=x-2上,点B1,B2,…,Bn均在双曲线y=-$\frac{4}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-2,则a2016=1.
分析 根据点的分布特征,找出an的前几项,根据an的变化,可得出规律“a3n-2=-2,a3n-1=4,a3n=1,(n为正整数)”,结合该规律即可得出a2016的值.
解答 解:观察,发现规律:a1=-2,a2=4,a3=1,a4=-2,…,
∴a3n-2=-2,a3n-1=4,a3n=1,(n为正整数)
∵2016=672×3,
∴a2016=1.
故答案为:1.
点评 本题考查了一次函数图象上点的坐标特征、反比例函数图象上点的坐标特征以及规律型中的点的变化,解题的关键是找出规律“a3n-2=-2,a3n-1=4,a3n=1,(n为正整数)”.本题属于基础题,难度不大,根据An、Bn点的特征列出an的部分值,根据该部分数据发现变化规律,再结合变化规律解决问题.

练习册系列答案
相关题目
16.如果$\frac{6sinα-2cosα}{2sinα+cosα}$=2,那么tanα=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
17.已知a,b是一元二次方程x2-2x-1=0的两个实数根,则代数式(a-b)(a+b-2)+ab的值等于( )
| A. | -1 | B. | 1 | C. | ±8$\sqrt{2}$-1 | D. | ±8$\sqrt{2}$+1 |
14. 如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )
如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )
 如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )
如图,AB∥CD,AC平分∠BCD,∠A=40°,则∠B的度数为( )| A. | 90° | B. | 100° | C. | 110° | D. | 120° |
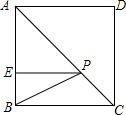 如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是2$\sqrt{34}$cm.
如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是2$\sqrt{34}$cm.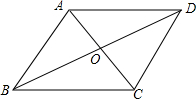 如图所示,在菱形ABCD中,∠BAD=120°,AB=4.
如图所示,在菱形ABCD中,∠BAD=120°,AB=4.