题目内容
11.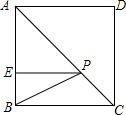 如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是2$\sqrt{34}$cm.
如图,正方形ABCD的边长为10cm,E是AB上一点,BE=4cm,P是对角线AC上一动点,则PB+PE的最小值是2$\sqrt{34}$cm.
分析 直接利用正方形的性质,得出B,D点关于直线AC对称,连接BD,ED,BP,进而利用勾股定理得出答案.
解答  解:如图所示:连接BD,DE,BP,
解:如图所示:连接BD,DE,BP,
由题意可得:B,D点关于直线AC对称,则P点是ED与AC的交点,
∵正方形ABCD的边长为10cm,BE=4cm,
∴AE=6cm,AD=10cm,
则EP+BP=ED=$\sqrt{1{0}^{2}+{6}^{2}}$=2$\sqrt{34}$(cm).
故答案为:2$\sqrt{34}$.
点评 此题主要考查了利用轴对称求最短路线以及正方形的性质,正确得出P点位置是解题关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
19.关于函数y=$\frac{6}{x}$ 有如下结论:①函数图象一定经过点(-2,-3);②函数图象在第一、三象限;③函数值y随x的增大而增大,这其中正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
3.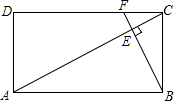 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
 如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )
如图,矩形ABCD中,F是DC上一点,BF⊥AC,垂足为E,$\frac{AD}{AB}=\frac{1}{2}$,△CEF的面积为S1,△AEB的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值等于( )| A. | $\frac{1}{16}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{25}$ |
1.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.已知1微米相当于1米的一百万分之一,则2.5微米用科学记数可表示为( )
| A. | 2.5×10-7米 | B. | 2.5×10-6米 | C. | 2.5×107米 | D. | 2.5×106米 |
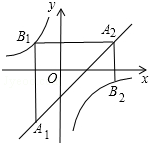 如图,已知点A1,A2,…,An均在直线y=x-2上,点B1,B2,…,Bn均在双曲线y=-$\frac{4}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-2,则a2016=1.
如图,已知点A1,A2,…,An均在直线y=x-2上,点B1,B2,…,Bn均在双曲线y=-$\frac{4}{x}$上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-2,则a2016=1.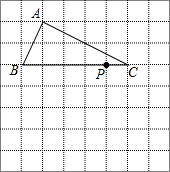 如图,将三角形ABC放在每个小正方形的边长为1的网格中,点A,点B,点C,点P均落在格点上.
如图,将三角形ABC放在每个小正方形的边长为1的网格中,点A,点B,点C,点P均落在格点上.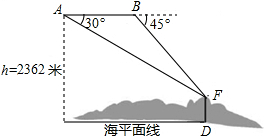 国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图,在一次巡航过程中,巡航飞机飞行高度为2362米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1464米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414)
国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图,在一次巡航过程中,巡航飞机飞行高度为2362米,在点A测得高华峰顶F点的俯角为30°,保持方向不变前进1464米到达B点后测得F点俯角为45°,请据此计算钓鱼岛的最高海拔高度多少米.(结果保留整数,参考数值:$\sqrt{3}$=1.732,$\sqrt{2}$=1.414)