Question

10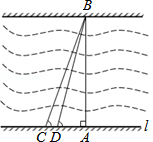．黄冈市为了改善市区交通状况，计划修建一座新大桥．如图，新大桥的两端位于A、B两点，小张为了测量A、B之间的河宽，在垂直于新大桥AB的直线型道路l上测得如下数据：∠BDA=76.1°，∠BCA=68.2°，CD=82米．求AB的长（精确到0.1米）．
参考数据：sin76.1°≈0.97，cos76.1°≈0.24，tan76.1°≈4.0；sin68.2°≈0.93，cos68.2°≈0.37，tan68.2°≈2.5．

Answer 1

分析 设AD=x米，则AC=（x+82）米．在Rt△ABC中，根据三角函数得到AB=2.5（x+82），在Rt△ABD中，根据三角函数得到AB=4x，依此得到关于x的方程，进一步即可求解．

解答 解：设AD=x米，则AC=（x+82）米．在Rt△ABC中，tan∠BCA=$\frac{AB}{AC}$，
∴AB=AC•tan∠BCA=2.5（x+82）．在Rt△ABD中，tan∠BDA=$\frac{AB}{AD}$，
∴AB=AD•tan∠BDA=4x．∴2.5（x+82）=4x，解得x=$\frac{410}{3}$，
∴AB=4x=4×$\frac{410}{3}$≈546.7，
答：AB的长约为546.7米．

点评 此题考查了解直角三角形的应用，主要是三角函数的基本概念及运算，关键是用数学知识解决实际问题．