题目内容
20. 如图所示的两段弧中,位于上方的弧半径为r上,下方的弧半径为r下,则r上<r下.(填“<”“=”“>”)
如图所示的两段弧中,位于上方的弧半径为r上,下方的弧半径为r下,则r上<r下.(填“<”“=”“>”)
分析 利用垂径定理,分别作出两段弧所在圆的圆心,从而得到两圆的半径,然后比较两个圆的半径即可.
解答 解:如图,r上<r下.
故答案为:<.
点评 本题考查了弧长公式:圆周长公式:C=2πR (2)弧长公式:l=$\frac{n•π•R}{180}$(弧长为l,圆心角度数为n,圆的半径为R);正确区分弧、弧的度数、弧长三个概念,度数相等的弧,弧长不一定相等,弧长相等的弧不一定是等弧,只有在同圆或等圆中,才有等弧的概念,才是三者的统一.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.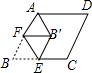 如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )
如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )
 如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )
如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | 2+$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
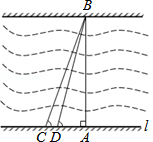 黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).
黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).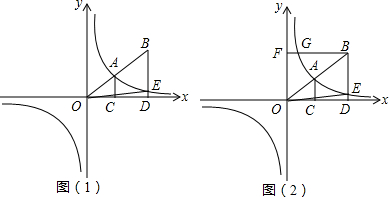
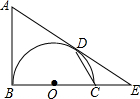 如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.