题目内容
18. 由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该面的夹角分别是30°和45°(如图),试确定生命所在点C的深度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1)
由于发生山体滑坡灾害,武警救援队火速赶往灾区救援,探测出某建筑物废墟下方点C处有生命迹象.在废墟一侧地面上探测点A、B相距2米,探测线与该面的夹角分别是30°和45°(如图),试确定生命所在点C的深度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1)
分析 首先分析图形:根据题意构造直角三角形;本题涉及多个直角三角形,应利用其公共边构造关系式,进而可求出答案.
解答 解:如图,过点C作CD⊥AB,交AB延长线于点D,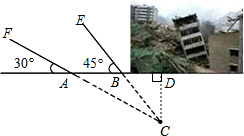
由题意知,∠CAD=30°,∠CBD=45°,
设CD=x米,
∴BD=CD=x米,
∵AB=2米,
∴AD=x+2米,
在RT△ACD中,∵tan∠CAD=$\frac{CD}{AD}$,
∴$\frac{x}{x+2}$=$\frac{\sqrt{3}}{3}$,
解得:x=$\sqrt{3}$+1≈2.7.
答:确定生命所在点C的深度为2.7米.
点评 考查了解直角三角形的应用,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
6. 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片
ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2$\sqrt{5}$.以上结论中,你认为正确的是( )
 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2$\sqrt{5}$.以上结论中,你认为正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
13.在平行四边形、矩形、菱形、正方形中是轴对称图形的有( )
| A. | 4个 | B. | 3 个 | C. | 2个 | D. | 1个 |
3.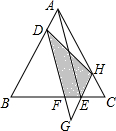 如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )
如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )
 如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )
如图,△ABC是正三角形,D,E分别是AB,BC上的点,其中CE=$\frac{1}{4}$CB,以AD,AE为邻边向下作一个平行四边形ADGE,DG交BC于点F,延长GE交AC于点H,连结DH,若S△BDF=9,S△GEF=1那么四边形DFEH的面积为( )| A. | 6 | B. | $\frac{16}{3}$ | C. | $\frac{25}{3}$ | D. | 7 |
7.下列方程中一定是一元二次方程的是( )
| A. | x2-6x=x2+9 | B. | (x-1)(x+2)=0 | C. | ax2-6x=0 | D. | (a-3)x2=5 |
 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°. 如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)
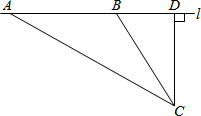
如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)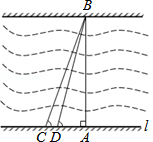 黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).
黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).