题目内容
20.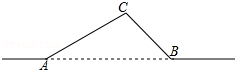 如图,一条光纤线路从A地到B地需要经过C地,图中AC=40千米,
如图,一条光纤线路从A地到B地需要经过C地,图中AC=40千米,∠CAB=30°,∠CBA=45°,因线路整改需要,将从A地到B地之间铺设一条笔直的光纤线路.
(1)求新铺设的光纤线路AB的长度;(结果保留根号)
(2)问整改后从A地到B地的光纤线路比原来缩短了多少千米?(结果保留根号)
分析 (1)过C作CD⊥AB,交AB于点D,利用∠CAD的正弦和余弦分别求出CD、AD,再利用∠CBA的正切求出BD,然后根据AB=AD+BD计算即可得解;
(2)利用勾股定理列式求出BC,然后列式计算即可得解.
解答 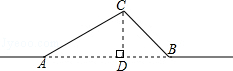 解:(1)过C作CD⊥AB,交AB于点D,
解:(1)过C作CD⊥AB,交AB于点D,
在Rt△ACD中,CD=AC•sin∠CAD=AC•sin30°=40×$\frac{1}{2}$=20(千米),
AD=AC•cos∠CAD=AC•cos30°=40×$\frac{\sqrt{3}}{2}$=20$\sqrt{3}$(千米),
在Rt△BCD中,BD=$\frac{CD}{tan∠CBA}$=$\frac{20}{tan45°}$=$\frac{20}{1}$=20(千米),
∴AB=AD+DB=20$\sqrt{3}$+20=20($\sqrt{3}$+1)(千米),
则新铺设的光纤线路AB的长度20($\sqrt{3}$+1)(千米);
(2)在Rt△BCD中,根据勾股定理得:BC=$\sqrt{C{D}^{2}+B{D}^{2}}$=$\sqrt{2{0}^{2}+2{0}^{2}}$=20$\sqrt{2}$(千米),
所以AC+CB-AB=40+20$\sqrt{2}$-20($\sqrt{3}$+1)=20(1+$\sqrt{2}$-$\sqrt{3}$)(千米),
则整改后从A地到B地的光纤线路比原来缩短了20(1+$\sqrt{2}$-$\sqrt{3}$)千米.
点评 本题考查了解直角三角形的应用,主要利用了锐角三角函数,作辅助线构造出直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道L上确定点D,使CD与L垂直,测得CD的长等于24米,在L上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.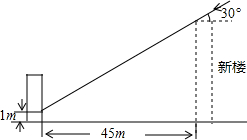 为了解决楼房之间的采光问题,某市有关部门规定:两幢楼房之间的最小距离要使中午12时不能遮光.如图,旧楼的一楼窗台高1m,现计划在旧楼正南方45m处建一幢新楼.已知该市冬天中午12时阳光从正南方照射的光线与水平线的夹角最小为30°,问新楼房最高可建多少米?
为了解决楼房之间的采光问题,某市有关部门规定:两幢楼房之间的最小距离要使中午12时不能遮光.如图,旧楼的一楼窗台高1m,现计划在旧楼正南方45m处建一幢新楼.已知该市冬天中午12时阳光从正南方照射的光线与水平线的夹角最小为30°,问新楼房最高可建多少米? 如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)
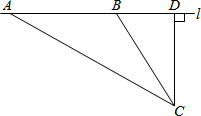
如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)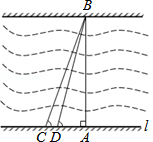 黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).
黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).