题目内容
1.要使关于x的方程$\frac{x+1}{x+2}-\frac{x}{x-1}=\frac{a}{(x+2)(x-1)}$的解是正数,a的取值范围是a<-1且a≠-3.分析 先解关于x的分式方程,求得x的值,然后再依据“解是正数”建立不等式求a的取值范围.
解答 解:去分母得:(x+1)(x-1)-x(x+2)=a,解得x=-$\frac{a+1}{2}$;
因为这个解是正数,所以-$\frac{a+1}{2}$>0,即a<-1;
又因为分式方程的分母不能为零,即-$\frac{a+1}{2}$≠1且-$\frac{a+1}{2}$≠-2,所以a≠±3;
则a的取值范围是a<-1且a≠-3;
故答案为:a<-1且a≠-3.
点评 此题考查了分式方程的解,由于我们的目的是求a的取值范围,根据方程的解列出关于a的不等式.另外,解答本题时,易漏掉分母不等于0这个隐含的条件,这应引起足够重视.

练习册系列答案
相关题目
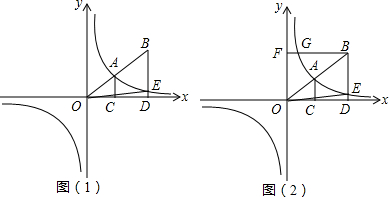
6. 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片
ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2$\sqrt{5}$.以上结论中,你认为正确的是( )
 如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片
如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:
①四边形CFHE是菱形;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;
④当点H与点A重合时,EF=2$\sqrt{5}$.以上结论中,你认为正确的是( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
13.在平行四边形、矩形、菱形、正方形中是轴对称图形的有( )
| A. | 4个 | B. | 3 个 | C. | 2个 | D. | 1个 |
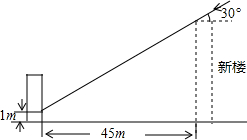 为了解决楼房之间的采光问题,某市有关部门规定:两幢楼房之间的最小距离要使中午12时不能遮光.如图,旧楼的一楼窗台高1m,现计划在旧楼正南方45m处建一幢新楼.已知该市冬天中午12时阳光从正南方照射的光线与水平线的夹角最小为30°,问新楼房最高可建多少米?
为了解决楼房之间的采光问题,某市有关部门规定:两幢楼房之间的最小距离要使中午12时不能遮光.如图,旧楼的一楼窗台高1m,现计划在旧楼正南方45m处建一幢新楼.已知该市冬天中午12时阳光从正南方照射的光线与水平线的夹角最小为30°,问新楼房最高可建多少米? 如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)
如图,小明想测量学校教学楼的高度,教学楼AB的后面有一建筑物CD,他测得当光线与地面成22°的夹角时,教学楼在建筑物的墙上留下高2m高的影子CE;而当光线与地面成45°的夹角时,教学楼顶A在地面上的影子F与墙角C有13m的距离(点B,F,C在同一条直线上)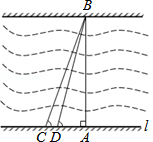 黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).
黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).