题目内容
5. 在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…,则S5的值为128.
在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…,则S5的值为128.
分析 结合正方形的性质结合直线的解析式可得出:A2B1=OC1,A3B2=C1C2,A4B3=C2C3,…,结合三角形的面积公式即可得出:S1=$\frac{1}{2}$$O{{C}_{1}}^{2}$=$\frac{1}{2}$,S2=$\frac{1}{2}{C}_{1}{{C}_{2}}^{2}$=2,S3=$\frac{1}{2}{C}_{2}{{C}_{3}}^{2}$=8,…,根据面积的变化可找出变化规律“Sn=22n-3(n为正整数)”,依此规律即可得出结论.
解答 解:令一次函数y=x+1中x=0,则y=1,
∴点A1的坐标为(0,1),OA1=1.
∵四边形AnBnCnCn-1(n为正整数)均为正方形,
∴A1B1=OC1=1,A2B2=C1C2=2,A3B3=C2C3=4,….
令一次函数y=x+1中x=1,则y=2,
即A2C1=2,
∴A2B1=A2C1-A1B1=1=A1B1,
∴tan∠A2A1B1=1.
∵AnCn-1⊥x轴,
∴tan∠An+1AnBn=1.
∴A2B1=OC1,A3B2=C1C2,A4B3=C2C3,….
∴S1=$\frac{1}{2}$$O{{C}_{1}}^{2}$=$\frac{1}{2}$,S2=$\frac{1}{2}{C}_{1}{{C}_{2}}^{2}$=2,S3=$\frac{1}{2}{C}_{2}{{C}_{3}}^{2}$=8,…,
∴Sn=22n-3(n为正整数).
当n=5时,S5=27=128.
故答案为:128.
点评 本题考查了一次函数图象上点的坐标特征、正方形的性质、三角形的面积公式以及规律型中得坐标的变化,解题的关键是找出“Sn=22n-3(n为正整数)”.本题属于中档题,难度不大,但转化过程较繁琐,用到知识点较多,好在该题为填空题,可以减少不少证明过程,可直接拿来应用.解决该题型题目时,找出面积的变化规律是关键.

 名校课堂系列答案
名校课堂系列答案| A. | 4个 | B. | 3 个 | C. | 2个 | D. | 1个 |
| A. | 7 | B. | 4 | C. | ±$\sqrt{3}$ | D. | ±3 |
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
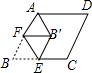 如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )
如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | 2+$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
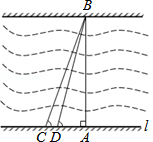 黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).
黄冈市为了改善市区交通状况,计划修建一座新大桥.如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求AB的长(精确到0.1米).