题目内容
18.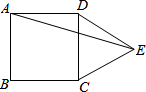 如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.
如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.
分析 由于四边形ABCD是正方形,△DCE是正三角形,由此可以得到AD=DE,接着利用正方形和正三角形的内角的性质即可求解.
解答 解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
又∵△DCE是正三角形,
∴DE=AD,∠EDC=60°,
∴△ADE是等腰三角形,∠ADE=90°+60°=150°,
∴∠AED=15°.
故答案为:15°.
点评 此题主要考查了正方形和等边三角形的性质,同时也利用了三角形的内角和,解题首先利用正方形和等边三角形的性质证明等腰三角形,然后利用等腰三角形的性质即可解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.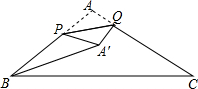 如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
 如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )
如图,在△ABC中,AB=AC=2,∠ABC=30°,点P、Q分别在边AB、AC上,将△APQ沿PQ翻折,点A落到点A′处,则线段BA′长度的最小值是( )| A. | 2$\sqrt{3}$-2 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
6. 如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
 如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
10.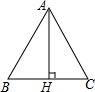 如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
 如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )
如图,等边△ABC的高AH等于$\sqrt{3}$,那么该三角形的面积为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
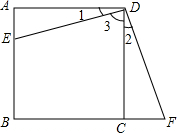 如图所示,点E是矩形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F,DE=DF.求证:矩形ABCD是正方形.
如图所示,点E是矩形ABCD的边AB上任意一点,过点D作DF⊥DE交BC的延长线于点F,DE=DF.求证:矩形ABCD是正方形.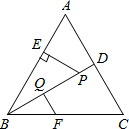 如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,求PE的长.
如图,△ABC是等边三角形,P是∠ABC的平分线BD上一点,PE⊥AB于点E,线段BP的垂直平分线交BC于点F,垂足为点Q.若BF=2,求PE的长. 已知:直线y=-x-4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为-2
已知:直线y=-x-4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为-2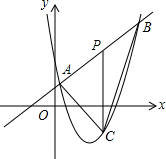 如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.
如图,直线y=x+4和抛物线y=ax2+bx+12(a≠0)相交于A(1,5)和B(8,n),点P是线段AB上异于A,B的动点,过点P作PC⊥x轴,交抛物线于点C.