题目内容
3.阅读材料:若m2-2mn+2n2-2n+1=0,求m、n的值.解:∵m2-2mn+2n2-2n+1=0,∴(m2-2mn+n2)+(n2-2n+1)=0
∴(m-n)2+(n-1)2=0,∴(m-n)2=0,(n-1)2=0,∴n=1,m=1.
根据你的观察,探究下面的问题:
(1)已知x2+2xy+2y2+2y+1=0,求x、y的值;
(2)已知a,b,c是△ABC的三边长,满足a2+b2=12a+8b-52,且△ABC是等腰三角形,求c的值.
分析 (1)已知等式整理后,利用完全平方公式变形,再利用非负数的性质求出x与y的值即可;
(2)已知等式整理后,利用完全平方公式变形,再利用非负数的性质求出a与b的值,即可确定出c的值.
解答 解:(1)已知等式整理得:(x+y)2+(y+1)2=0,
∴x=1,y=-1;
(2)已知等式整理得:(a-6)2+(b-4)2=0,
解得:a=6,b=4,
由△ABC为等腰三角形,得到三边为6,6,4或4,4,6,
则c的值为4或6.
点评 此题考查了因式分解的应用,以及非负数的性质,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
相关题目
11.下列说法中正确的个数有( )
①有一个角为60°的等腰三角形是等边三角形;
②三边长为$\sqrt{14}$,$\sqrt{5}$,3的三角形为直角三角形;
③等腰三角形的两条边长为2,4,则等腰三角形的周长为10或8;
④一边上的中线等于这边长的一半的三角形是等腰直角三角形.
①有一个角为60°的等腰三角形是等边三角形;
②三边长为$\sqrt{14}$,$\sqrt{5}$,3的三角形为直角三角形;
③等腰三角形的两条边长为2,4,则等腰三角形的周长为10或8;
④一边上的中线等于这边长的一半的三角形是等腰直角三角形.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.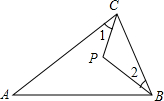 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
 如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
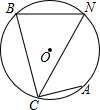 如图,⊙O是△BCN的外接圆,弦AC⊥BC,点N是$\widehat{AB}$的中点,∠BNC=60°,求$\frac{BN}{BC}$的值.
如图,⊙O是△BCN的外接圆,弦AC⊥BC,点N是$\widehat{AB}$的中点,∠BNC=60°,求$\frac{BN}{BC}$的值.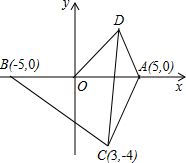 如图,在平面直角坐标系中,点A为(5,0),点B为(-5,0),点C为(3,-4),点D为第一象限上的一个动点,且OD=5.
如图,在平面直角坐标系中,点A为(5,0),点B为(-5,0),点C为(3,-4),点D为第一象限上的一个动点,且OD=5.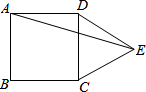 如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.
如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.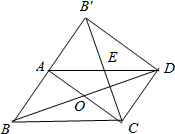 如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.
如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.