题目内容
6. 如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
如图是“明清影视城”的圆弧形门,这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.则这个圆弧形门的最高点离地面的高度是520 cm.
分析 连接OF,交AC于点E,设圆O的半径为R,根据勾股定理列出方程,解方程即可.
解答 解:连接OF,交AC于点E,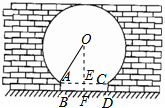
∵BD是⊙O的切线,
∴OF⊥BD,
∵四边形ABDC是矩形,
∴AD∥BD,
∴OE⊥AC,EF=AB,
设圆O的半径为R,在Rt△AOE中,AE=$\frac{AC}{2}$=$\frac{BD}{2}$=100,
OE=R-AB=R-20,
∵AE2+OE2=OA2,
∴1002+(R-20)2=R2,
解得,R=260.
260×2=520(cm).
故答案为:520.
点评 本题考查的是垂径定理的应用,掌握平分弦(不是直径)的直径垂直于弦是解题的关键,注意勾股定理的灵活运用.

练习册系列答案
相关题目
1.下列各图中,能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
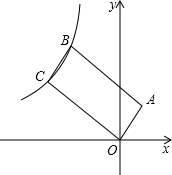 如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.
如图,反比例函数y=$\frac{k}{x}$(x<0)的图象经过平行四边形OABC的两个顶点B,C,若点A的坐标为(1,2),AB=$\sqrt{5}$BC,则反比例函数的解析式为y=-$\frac{12}{x}$或y=-$\frac{119}{25x}$.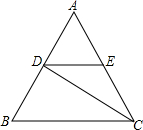 如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为4,则EC的边长是2.
如图,△ABC是等边三角形,CD是∠ACB的平分线,过点D作BC的平行线交AC于点E,已知△ABC的边长为4,则EC的边长是2.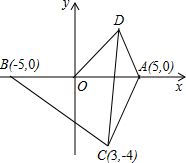 如图,在平面直角坐标系中,点A为(5,0),点B为(-5,0),点C为(3,-4),点D为第一象限上的一个动点,且OD=5.
如图,在平面直角坐标系中,点A为(5,0),点B为(-5,0),点C为(3,-4),点D为第一象限上的一个动点,且OD=5.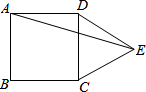 如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.
如图,在正方形ABCD的外侧,作等边三角形CDE,则∠AED的度数为15°.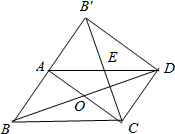 如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2.
如图所示,在平行四边形ABCD纸片中,AC⊥AB,AC与BD相交于点O,将△ABC沿对角线AC翻折得到△AB′C,若四边形ABCD的面积为12cm2,则翻折后纸片重叠部分的面积是3cm2. 已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.
已知长度分别为3,6,2x-1的三条正整数长线段可以组成一个三角形.